|x+19|+|x+5|+|x+2020|=5x(*)

+)Ta có:|x+19|\(\ge\)0;|x+5|\(\ge\)0;|x+2020|\(\ge\)0

=>VT(*)=|x+19|+|x+5|+|x+2020|\(\ge\)0

Mà |x+19|+|x+5|+|x+2020|=5x

=>5x\(\ge\)0

=>x\(\ge\)0

+)Ta lại có:x\(\ge\)0=>x+19\(\ge\)19=>|x+19|=x+19

                    x\(\ge\)0=>x+5\(\ge\)5=>|x+5|=x+5

                   x\(\ge\)0=>x+2020\(\ge\)2020=>|x+2020|=x+2020

=>VT(*)=x+19+x+5+x+2020=5x

              x+x+x+19+5+2020=5x

             3x+2044        =5x

                  2044        =5x-3x

                  2044        =2x

               => 2x            =2044

                   x             =\(\frac{2044}{2}=1022\)\(\in\)Z

Vậy x=1022

Chúc bn học tốt

cảm ơn bạn nha!!!

TH1: x + y + z $\ne$ 0

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{y+z+1}$ = $\frac{y}{x+z+2}$ = $\frac{z}{x+y-3}$ = $\frac{x+y+z}{y+z+1+x+z+2+x+y-3}$ 

              = $\frac{x+y+z}{x+y+z+x+y+z}$ = $\frac{x+y+z}{2(x+y+z)}$ = $\frac{1}{2}$ 

⇒ x + y + z = $\frac{1}{2}$

⇒ x + y       = $\frac{1}{2}$ - z

    x + z        = $\frac{1}{2}$ - y

    y + z        = $\frac{1}{2}$ - x

Thay y + z + 1 = $\frac{1}{2}$ - x + 1

⇒ $\frac{x}{\frac{1}{2}-x+1}$ = $\frac{1}{2}$

⇒ 2x = $\frac{1}{2}$ - x + 1

⇒ 2x + x = $\frac{1}{2}$ + 1

⇒  3x   =  $\frac{3}{2}$

⇒   x    = $\frac{1}{2}$

Thay x + z + 2 = $\frac{1}{2}$ - y + 2

⇒ $\frac{y}{\frac{1}{2}-y+2}$ = $\frac{1}{2}$

⇒ 2y = $\frac{1}{2}$ - y + 2

⇒ 2y + y = $\frac{1}{2}$ + 2

⇒   3y  = $\frac{5}{2}$

⇒     y   = $\frac{5}{6}$

Thay x + y - 3 = $\frac{1}{2}$ - z - 3

⇒ $\frac{z}{\frac{1}{2}-z-3}=$\frac{1}{2}$

⇒ 2z = $\frac{1}{2}$ - z - 3

⇒ 2z + z = $\frac{1}{2}$ - 3

⇒  3z  = $\frac{-5}{2}$

⇒   z   = $\frac{-5}{6}$

TH2: x + y + z = 0

⇒ $\frac{x}{y+z+1}$ = $\frac{y}{x+z+2}$ = $\frac{z}{x+y-3}$ = 0

⇒ x = y = z = 0

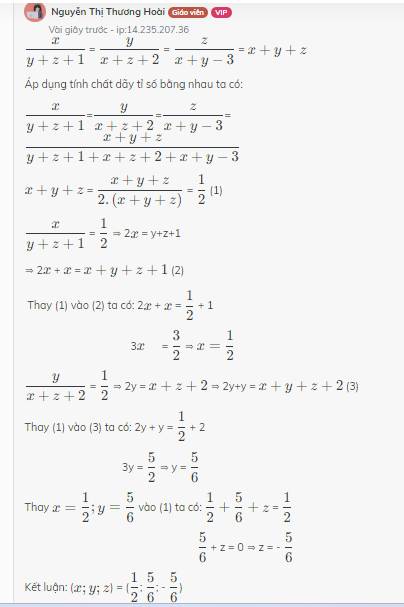
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934

Ta có : \(\frac{3}{x-1}=\frac{4}{y-2}=\frac{5}{z-3}\Rightarrow1:\frac{3}{x-1}=1:\frac{4}{y-2}=1:\frac{5}{z-3}\)

\(\Rightarrow\frac{x-1}{3}=\frac{y-2}{4}=\frac{z-3}{5}\)

Đặt \(\frac{x-1}{3}=\frac{y-2}{4}=\frac{z-3}{5}=k\Rightarrow\hept{\begin{cases}x=3k+1\\y=4k+2\\z=5k+3\end{cases}}\)

Khi đó x + y + z = 18 

<=> 3k + 1 + 4k + 2 + 5k + 3 = 18

=> 12k + 6 = 18

=> 12k = 12

=> k = 1

=> x = 4 ; y = 6 ; z = 8

                                                  Bài giải

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :

\(\frac{3}{x-1}=\frac{4}{y-2}=\frac{5}{z-3}=\frac{3+4+5}{x-1+y-2+z-3}=\frac{12}{12}=1\)

\(\Rightarrow\text{ }\hept{\begin{cases}x=3\text{ : }1+1=4\\y=4\text{ : }1+2=6\\z=5\text{ : }1+3=8\end{cases}}\)

\(\Rightarrow\text{ }x=4\text{ ; }y=6\text{ ; }z=8\)

Theo tính chất của dãy tỉ số bằng nhau thì : 

\(\frac{3}{x-1}=\frac{4}{y-2}=\frac{5}{z-3}=\frac{3+4+5}{x-1+y-2+z-3}=\frac{12}{18-6}=1\)

\(< =>\hept{\begin{cases}\frac{3}{x-1}=1< =>x-1=3\\\frac{4}{y-2}=1< =>y-2=4\\\frac{5}{z-3}=1< =>z-3=5\end{cases}}\)

\(< =>\hept{\begin{cases}x=3+1=4\\y=4+2=6\\z=5+3=8\end{cases}}\)

Vậy

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{x}{y+z-5}=\frac{y}{x+z+3}=\frac{z}{x+y+2}=\frac{x+y+z}{y+z-5+x+z+3+x+y+2}=\frac{x+y+z}{2x+2y+2z}=\frac12\)

=>\(\begin{cases}y+z-5=2x\\ x+z+3=2y\\ x+y+2=2z\end{cases}\Rightarrow\begin{cases}y+z=2x+5\\ y+z=2y-3\\ x+y=2z-2\end{cases}\)

\(\frac{x}{y+z-5}=\frac12\left(x+y+z\right)\)

=>\(\frac12\left(x+y+z\right)=\frac12\)

=>x+y+z=1

*Ta có: x+y+z=1

=>z+2z-2=1

=>3z-2=1

=>3z=3

=>z=1

*Ta có: x+y+z=1

=>y+2y-3=1

=>3y=4

=>\(y=\frac43\)

*Ta có: x+y+z=1

=>x+2x+5=1

=>3x+5=1

=>3x=-4

=>\(x=-\frac43\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{x}{y+z-5}=\frac{y}{x+z+3}=\frac{z}{x+y+2}=\frac{x+y+z}{y+z-5+x+z+3+x+y+2}=\frac{x+y+z}{2x+2y+2z}=\frac12\)

=>\(\begin{cases}y+z-5=2x\\ x+z+3=2y\\ x+y+2=2z\end{cases}\Rightarrow\begin{cases}y+z=2x+5\\ y+z=2y-3\\ x+y=2z-2\end{cases}\)

\(\frac{x}{y+z-5}=\frac12\left(x+y+z\right)\)

=>\(\frac12\left(x+y+z\right)=\frac12\)

=>x+y+z=1

*Ta có: x+y+z=1

=>z+2z-2=1

=>3z-2=1

=>3z=3

=>z=1

*Ta có: x+y+z=1

=>y+2y-3=1

=>3y=4

=>\(y=\frac43\)

*Ta có: x+y+z=1

=>x+2x+5=1

=>3x+5=1

=>3x=-4

=>\(x=-\frac43\)

Nhân đa thức vs đa thức.

Chuyển các hạng tử chứa x sang vế trái, vế còn lại là các hạng tử là hằng số.

Vế trái:Đặt x làm nhân tử chung; vế phải tính.

Vì 4 thuộc Z nên mỗi hạng tử ở vế trái đều thuộc Z và thuộc ước của 4.

Thay x lần lượt bằng 1;-1;2;-2;4;-4(ước của 4) vào vế trái. Trường hợp nào x;y thỏa mãn đề bài là đúng.

8/15 - 2/15 : x = 0,2

2/15 : x = 8/15 - 0,2

2/15 : x = 1/3

x = 2/15 : 1/3

x = 2/5

em làm ngược lại thoi 

2/15 : x = 8 /15 - 0,2

x = 2/15:( 8 /15 - 0,2)

Vì \(\left|x+2\right|;\left|y-7\right|\ge0\forall x;y\)

mà \(\left|x+2\right|+\left|y-7\right|=0\)

\(\Rightarrow\hept{\begin{cases}x+2=0\\y-7=0\end{cases}\Rightarrow}\hept{\begin{cases}x=-2\\y=7\end{cases}}\)

Vậy ( x; y ) = ( -2; 7 )

\(\left|x+2\right|+\left|y-7\right|=0\)

\(\Rightarrow\left|x+2\right|=\left|y-7\right|=0\Rightarrow\hept{\begin{cases}x+2=0\\y-7=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2\\y=7\end{cases}}\)

a.

\(2x-x^2+7=-\left(x^2-2x+1\right)+8=-\left(x-1\right)^2+8\le8\)

\(\Rightarrow2+\sqrt{2x-x^2+7}\le2+\sqrt{8}=2+2\sqrt{2}\)

\(\Rightarrow\dfrac{3}{2+\sqrt{2x-x^2+7}}\ge\dfrac{3}{2+2\sqrt{2}}=\dfrac{3\sqrt{2}-3}{2}\)

\(A_{min}=\dfrac{3\sqrt{2}-3}{2}\) khi \(x=1\)

b. ĐKXĐ: \(x\le1\)

\(B=-\left(1-x-\sqrt{2\left(1-x\right)}+\dfrac{1}{2}-\dfrac{1}{2}-1\right)\)

\(B=-\left(1-x-\sqrt{2\left(1-x\right)}+\dfrac{1}{2}\right)+\dfrac{3}{2}\)

\(B=-\left(\sqrt{1-x}-\dfrac{\sqrt{2}}{2}\right)^2+\dfrac{3}{2}\le\dfrac{3}{2}\)

\(B_{max}=\dfrac{3}{2}\) khi\(x=\dfrac{1}{2}\)