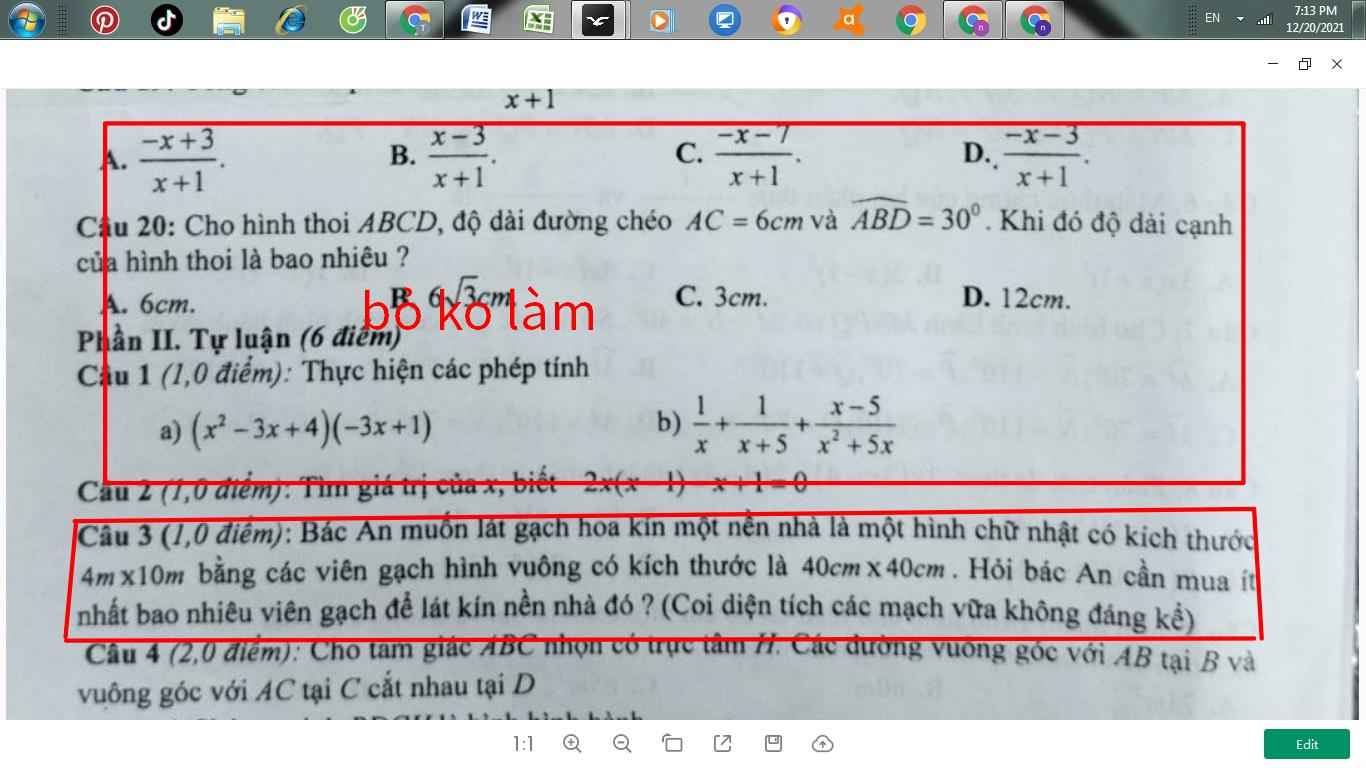
mọi người làm hộ mik bài 3 phần tự luận nha !!!
giải hộ mik phần tự luận bài 3 nha,cảm ơn trước mik cần gấp lắm

Bài 4:
Ta có: \(A=x^2+4x+y^2-5y+20\)
\(=x^2+4x+4+y^2-5y+\dfrac{25}{4}+\dfrac{39}{4}\)
\(=\left(x+2\right)^2+\left(y-\dfrac{5}{2}\right)^2+\dfrac{39}{4}\ge\dfrac{39}{4}\forall x,y\)
Dấu '=' xảy ra khi x=-2 và \(y=\dfrac{5}{2}\)
Đề bài: Viết đoạn văn nghị luận về truyền thống biết ơn của người Việt Nam. Chỉ ra câu rút gọn, câu đặc biệt, câu có thành phần trạng ngữ trong đoạn văn
Mọi người ơi, làm hộ mình nha mọi người. Cảm ơn mọi người nhiều
viết đoạn văn nghị luận xã hội về hạnh phúc
( tự làm ko dùng bài mạng nha mọi người )
Mọi người giúp mik bài 18 nhé đề bài mik để ở phần bình luận
Mọi người giúp mik với. Giúp mik 2 câu phần tự luận
Làm hộ em bài 2 phần tự luận giải cụ thể ra 
2:
Chiều cao là: 26*2:8=6,5cm
S2-S1=1/2*6,5*11-1/2*6,5*8=9,75cm2
Mọi người giúp mik bài 6 với, đề bài và câu hỏi mik để ở phần bình luận
\(\widehat{x'MC}=\widehat{xMN}\)(hai góc đối đỉnh
mà \(\widehat{xMN}=60^0\)
nên \(\widehat{x'MC}=60^0\)
Mz là phân giác của \(\widehat{x'MC}\)
=>\(\widehat{x'Mz}=\widehat{CMz}=\dfrac{60^0}{2}=30^0\)
Mz//Nt
=>\(\widehat{zMC}=\widehat{tNM}\)(hai góc đồng vị)
=>\(\widehat{tNM}=30^0\)
Nt là phân giác của góc y'NM
=>\(\widehat{y'NM}=2\cdot\widehat{tMN}=60^0\)
Mọi người làm hộ mik 3 câu này chi tiết không viết đáp án luôn nha mik đang rất gấp để nộp

Mọi người giúp mik câu 6,7,8,9 nhé, đề bài mik để ở phần bình luận.
Bài 7:
a:
Ta có: ΔABC đều
=>AB=AC=BC và \(\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^0\)
Xét ΔABC có \(\widehat{ACE}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACE}=\widehat{CAB}+\widehat{CBA}=120^0\)
Xét ΔACE có \(\widehat{ACE}>90^0\)
nên AE là cạnh lớn nhất trong ΔACE
=>AE>AC
=>AE>AB
b: Xét ΔCAE có CA=CE(=BC)
nên ΔCAE cân tại C
=>\(\widehat{CAE}=\dfrac{180^0-120^0}{2}=30^0\)
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
=>\(\widehat{HAC}=\dfrac{\widehat{BAC}}{2}=30^0\)
=>\(\widehat{HAC}=\widehat{CAE}\)
=>AC là phân giác của góc HAE
bài 9:
a: ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC
b: Xét ΔAHM vuông tại H có AM là cạnh huyền
nên AM là cạnh lớn nhất trong ΔAHM
=>AM>AH
Xét ΔAHM có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{AHM}+\widehat{HAM}=90^0+\widehat{HAM}\)
=>\(\widehat{AMB}>90^0\)
Xét ΔAMB có \(\widehat{AMB}>90^0\)
nên AB là cạnh lớn nhất trong ΔAMB
=>AB>AM
=>AB>AM>AH
=>AC>AM>AH