tìm tham số thực m để phương trình căn x2+5x+m bằng 3-x có nghiệm
Cho phương trình: x2 - 5x +m -1 = 0 (m là tham số). a) Giải phương trình trên khi m = -5. b) Tìm m để phương trình trên có hai nghiệm x1, X2 thỏa mãn: x1-x= 3. c) Tìm m để phưrơng trình trên có hai nghiệm x1, X2 thỏa mãn 2x, - 3x, = 5 d) Tìm m để phương trình trên có hai nghiệm x1, X2 thòa mãn (x - 1) +(x, -1) = 5 e) Tìm m đề phương trình trên có hai nghiệm x1, X2 thỏa mãn (x, - 1) +(x,-1) +2x,x, <5 g) Tìm m để phương trình trên có hai nghiệm x1, X2 thỏa mãn x <1
a: Khi m=-5 thì pt sẽ là x^2-5x-6=0
=>x=6 hoặc x=-1
b:
Δ=(-5)^2-4(m-1)=25-4m+4=-4m+29
Để pt có hai nghiệm thì -4m+29>=0
=>m<=29/4
x1-x2=3
=>(x1-x2)^2=9
=>(x1+x2)^2-4x1x2=9
=>5^2-4(m-1)=9
=>4(m-1)=25-9=16
=>m-1=4
=>m=5(nhận)
c: 2x1-3x2=5 và x1+x2=5
=>x1=4 và x2=1
x1*x2=m-1
=>m-1=4
=>m=5(nhận)
Cho phương trình m . 2 x 2 - 5 x + 6 + 2 1 - x 2 = 2 . 2 6 - 5 x + m . Tìm tất cả các giá trị thực của tham số m để phương trình có 4 nghiệm phân biệt
![]()
![]()
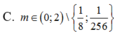
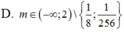
Cho phương trình m . 2 x 2 - 5 x + 6 + 2 1 - x 2 = 2 . 2 6 - 5 x . Tìm tất cả các giá trị thực của tham số m để phương trình có 4 nghiệm phân biệt.
A. m ∈ 0 ; 2
B. m ∈ 0 ; + ∞
C. m ∈ 0 ; 2 \ 1 8 ; 1 256
D. m ∈ - ∞ ; 2 \ 1 8 ; 1 256
Chọn C.
Phương pháp: Biến đổi đưa về phương trình tích.
Cách giải:
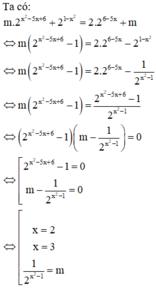
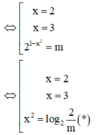
Vậy để phương trình đã cho có 4 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt khác 2 và 3.
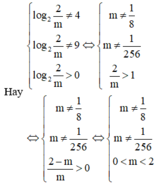
Cho phương trình m . 2 x 2 - 5 x + 6 + 2 1 - x 2 = 2 . 2 6 - 5 x + m (1). Tìm tất cả các giá trị thực của tham số m để phương trình có 4 nghiệm phân biệt
A. m ∈ ( 0 ; 2 )
B. m ∈ ( 0 ; + ∞ )
C. m ∈ ( 0 ; 2 ) \ { 1 8 ; 1 256 }
D. m ∈ ( - ∞ ; 2 ) \ { 1 8 ; 1 256 }
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
cho phương trình \(x^2+5x+3m-1=0\)(m là tham số)
tìm m để phương trình có 2 nghiệm x1,x2 thỏa mãn \(x_1^3-x_2^3+3x_1x_2=75\)
Cho phương trình bậc hai x2+5x+m-3=0 (∗∗) . (m là tham số. Tìm điều kiện của m để phương trình (*) có hai nghiệm x1, x2 thỏa mãn x1<2<x2
Δ=5^2-4(m-3)
=25-4m+12=-4m+27
Để phương trình có 2 nghiệm thì -4m+27>=0
=>m<=27/4
Theo đề, ta có: x1-2<0 và x2-2>0
=>(x1-2)(x2-2)<0
=>x1x2-2(x1+x2)+4<0
=>m-3-2*(-5)+4<0
=>m+1+10<0
=>m<-11
Tìm tất cả các giá trị thực của tham số m để phương trình x 2 − 5 x + 7 + 2 m = 0 có nghiệm thuộc đoạn [1;5]
A. 3 4 ≤ m ≤ 7
B. − 7 2 ≤ m ≤ − 3 8
C. 3 ≤ m ≤ 7
D. 3 8 ≤ m ≤ 7 2
Cho pt: x2 - 5x + m = 0 (m là tham số)
Tìm m để phương trình trên có 2 nghiệm x1, x2 thoả mãn: |x1 - x2| = 3
\(\Delta=25-4m\ge0\Rightarrow m\le\dfrac{25}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m\end{matrix}\right.\)
\(\left|x_1-x_2\right|=3\Leftrightarrow\left(x_1-x_2\right)^2=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=9\)
\(\Leftrightarrow25-4m=9\Rightarrow m=4\) (thỏa mãn)
Pt có 2 nghiệm
\(\to \Delta=(-5)^2-4.1.m=25-4m\ge 0\\\leftrightarrow 4m\le 25\\\leftrightarrow m\le\dfrac{25}{4}\)
Theo Viét
\(\begin{cases}x_1+x_2=5\\x_1x_2=m\end{cases}\)
\(|x_1-x_2|=3\\\leftrightarrow \sqrt{(x_1-x_2)^2}=3\\\leftrightarrow \sqrt{x_1^2+x_2^2-2x_1x_2}=3\\\leftrightarrow \sqrt{(x_1+x_2)^2-4x_1x_2}=3\\\leftrightarrow \sqrt{5^2-4m}=3\\\leftrightarrow 25-4m=9\\\leftrightarrow 4m=16\\\leftrightarrow m=4(TM)\)
Vậy \(m=4\) thỏa mãn hệ thức