Tìm số hạng đầu , công sai d và số hạng thứ 15 của cấp số cộng
(Un)=> U1+U5=14
U2+U6=
Tính số hạng đầu u 1 và công sai d của cấp số cộng ( u n ) biết u 1 + u 5 - u 3 = 10 u 1 + u 6 = 7
Cho cấp số cộng ( u n ) biết u 5 = 18 và 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 3 ; d = 2
B. u 1 = 2 ; d = 3
C. u 1 = 2 ; d = 2
D. u 1 = 2 ; d = 4
Đáp án D
u 5 = 18 ⇔ u 1 + 4 d = 18 ( 1 )
4 S n = S 2 n
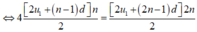
⇒ 2 u 1 - d = 0 ( 2 )
Từ (1) & (2) ta có u 1 = 2 ; d = 2
Cho cấp số cộng ( u n ) biết u 5 = 18 v à 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 2 , d = 4
B. u 1 = 2 , d = 3
C. u 1 = 2 , d = 2
D. u 1 = 3 , d = 2
Cho cấp số cộng u n biết u 5 = 18 và 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng.
A. u 1 = 2 , d = 4
B. u 1 = 2 , d = 3
C. u 1 = 2 , d = 2
D. u 1 = 3 , d = 2
Cho cấp số cộng u n có số hạng đầu u 1 = − 3 v à u 6 = 27 . Tìm công sai d.
A. d = 8
B. d = 6
C. d = 5
D. d = 7
Tìm số hạng đầu và công sai của các cấp số cộng sau, biết: u 1 - u 3 + u 5 = 10 u 1 + u 6 = 7
Ta có : u3 = u1 + 2d ;
u5 = u1 + 4d ;
u6 = u1 + 5d
Theo đề bài ta có :
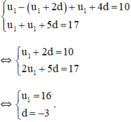
Tìm số hạng đầu u 1 và công bội q của các cấp số nhân u n , biết: u 2 + u 5 - u 4 = 10 u 3 + u 6 - u 5 = 20
Ta có:
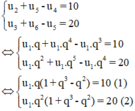
Lấy (2) chia (1) theo vế với vế ta được q = 2 thế vào (1):
(1) ⇔ 2u1(1 + 8 - 4) = 10 ⇔ u1 = 1
Vậy u1 = 1 và q = 2
Cho cấp số cộng u n có số hạng đầu u 1 = 3 và công sai d = 2 . Tính u 5
A. 11
B. 15
C. 12
D. 14
Chọn đáp án A
Ta có: u 5 = u 1 + 4 d = 3 + 4 . 2 = 11
Cho cấp số cộng ( u n ) có số hạng đầu u 1 = 3 và công sai d = 2 . Tính u 5
A. 11
B. 15
C. 12
D. 14
Chọn đáp án A
Ta có:
u 5 = u 1 + 4 d = 3 + 4 . 2 = 11