Cát tuyến là j ạ

Những câu hỏi liên quan
Cát tuyến là gì ạ??? tính chất thế nào??
Tuyến có nghĩa là đường thắng; cát nghĩa là cắt.
Cát tuyến là đường thẳng cắt một đường cong hoặc cắt một số đường thẳng cho trước.
Đúng 0
Bình luận (0)
Tuyến có nghĩa là đường thắng; cát nghĩa là cắt. Cát tuyến là đường thẳng cắt các đường khác (đường thẳng, đường tròn, đường cong....).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho đường tròn (O) cố định và điểm M cố định nằm ngoài (O). từ M kể các tiếp tuyến MA, MB đến (O) (A, B là các tiếp điểm) và vẽ cát tuyến MIJ không đi qua tâm O,( I,J ∈ (O), I nằm giữa M và J). CMR tứ giác MAOB nội tiếp ( Vẽ hình)
(mink đag cần gấp)
xét (O) có MA ,MB là các tiếp tuyến(A,B là tiếp điểm)
=>góc OAM=90 độ
góc OBM=90 độ
=>góc OAM+góc OBM=180 độ
2 góc này ở vị trí đối diện=> tứ giác MAOB nội tiếp
Đúng 0
Bình luận (0)
cho đươờng tròn (O;R) và điểm M nằm bên ngoài đường tròn qua M kẻ cát tuyến MAB với đường tròn tim quỹ tích trung điểm của dây AB khi cát tuyến MAB quay quanh M
mn giúp mik vs ạ![]()
Mọi người giúp với ạ.
Cho một đường tròn tâm O và một điểm S nằm ngoài đường tròn. Vẽ tiếp tuyến SA và cát tuyến SBC ( B nằm giữa ). Phân giác của góc BAC cắt BC tại D. Chứng minh :
a, SA2= SB.SC
b, SA=SD
c, Trong tất cả các cát tuyến từ S thì cát tuyến qua tâm O là dài nhất.
d. Cho SA = 20, SC = 50. Tính R (O).
Ai biết thì giải dùm với. Cảm ơn nhiều.
a) Ta có : Góc SAB = 1/2 sđ cung AB ( Góc tạo bởi tiếp tuyến và dây cung)
Góc SCA = 1/2 sđ cung AB (Góc nội tiếp)
=> Góc SAB = Góc SCA
Xét hai tam giác : \(\Delta SAB\)và \(\Delta SCA\)có : Góc ASC chung , Góc SAB = góc SCA
=> \(\Delta SAB~\Delta SCA\left(g.g\right)\)\(\Rightarrow\frac{SA}{SC}=\frac{SB}{SA}\Rightarrow SA^2=SB.SC\)
b) Ta có SDA là góc ngoài của tam giác ACD \(\Rightarrow SDA=DAC+DCA=DAC+\frac{1}{2}sdAB\)
Mặt khác, ta có ; \(SAD=BAD+\frac{1}{2}sdAB=DAC+\frac{1}{2}sdAB\)( Vì AD là tia phân giác)
Do đó góc SDA = góc SAD => Tam giác SAD cân tại S => SA = SD
Đúng 0
Bình luận (0)
Cho điểm A nằm ngoài đường tròn (O,R) với OARsqrt{2}Đường tròn tâm I đường kính OA cắt đường tròn (O) ở B và C.1) Chứng minh AB,AC là hai tiếp tuyến của đường tròn (O) và tính độ dài của AB, AC theo R2) Tứ giác ABOC là hình gì? Vì sao? 3) Đường thẳng OA cắt đường tròn (O) ở D và E ( D nằm giữa A và O). Kẻ cát tuyến AMN của đường tròn (O). Chứng minh AD.AEAM.AN hằng số 4) Khi cát tuyến AMN quay quanh A thì trung điểm K của đoạn MN di động trên đường cố định nào? Hãy chứng minh điều ấy5) Cát...
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O,R) với OA=R\(\sqrt{2}\)Đường tròn tâm I đường kính OA cắt đường tròn (O) ở B và C.
1) Chứng minh AB,AC là hai tiếp tuyến của đường tròn (O) và tính độ dài của AB, AC theo R
2) Tứ giác ABOC là hình gì? Vì sao?
3) Đường thẳng OA cắt đường tròn (O) ở D và E ( D nằm giữa A và O). Kẻ cát tuyến AMN của đường tròn (O). Chứng minh AD.AE=AM.AN= hằng số
4) Khi cát tuyến AMN quay quanh A thì trung điểm K của đoạn MN di động trên đường cố định nào? Hãy chứng minh điều ấy
5) Cát tuyến AMN cắt BC ở J. Chứng minh rằng O,K,J,I cùng nằm trên một đường tròn và AJ.AK=AB2

1) Do B, C cùng thuộc đường tròn đường kính AO nên \(\widehat{ABO}=\widehat{ACO}=90^o\) (Góc nội tiếp chắn nửa đường tròn)
Vậy nên AB, AC là các tiếp tuyến của đường tròn (O).
Xét tam giác vuông ABO có \(AO=R\sqrt{2};OB=R\)
Áp dụng định lý Pi-ta-go ta có:
\(AB=\sqrt{AO^2-BO^2}=R\)
Vậy thì AC = AB = R.
2) Ta thấy tứ giác ABOC có AB = BO = OC = CA = R nên nó là hình thoi.
Lại có \(\widehat{ABO}=90^o\) nên ABOC là hình vuông.
3) Xét tam giác ADC và tam gác ACE có:
Góc A chung
\(\widehat{ACD}=\widehat{AEC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung DC)
\(\Rightarrow\Delta ADC\sim\Delta ACE\left(g-g\right)\)
\(\Rightarrow\frac{AD}{AC}=\frac{AC}{AE}\Leftrightarrow AD.AE=AC^2=R^2\) = hằng số.
Hoàn toàn tương tự ta cũng có AM.AN = AB2 = R2 = hằng số.
Vậy nên AM.AN = AD.AE = R2.
4) Xét đường tròn (O), ta có K là trung điểm dây cung MN nên theo liên hệ đường kính dây cung, ta có: \(OK\perp MN\) hay \(\widehat{AKO}=90^o\)
Vậy thì K thuộc đường tròn đường kính OA.
Do AMN là cát tuyến nên K thuộc cung tròn BmC (trên hình vẽ).
5) Ta có ABOC là hình vuông nên AO và BC cắt nhau tại trung điểm mỗi đường.
Vậy thì BC qua tâm I.
Từ đó ta có \(\widehat{IJO}=90^o\)
Lại vừa chứng minh được \(\widehat{JKO}=90^o\).
Tứ giác IJKO có tổng hai góc đối bằng 180o nên IJKO là tứ giác nội tiếp hay O, K, I, J cùng thuộc một đường tròn.
Ta có AB = AC nên \(\widebat{AB}=\widebat{AC}\Rightarrow\widehat{BKA}=\widehat{CBA}=\widehat{JBA}\)
Vậy thì \(\Delta ABJ\sim\Delta AKB\left(g-g\right)\Rightarrow\frac{AB}{AK}=\frac{AJ}{AB}\Rightarrow AJ.AK=AB^2\)
Đúng 0
Bình luận (0)
cho đg tròn tâm O, R=6cm và điểm A cách O 10cm. từ A vẽ tiếp tuyến AB ( B là tiếp điểm) và cát tuyến ACD( A nằm giữa C D) I là trung điểm cd
vẽ hình hộ em ạ
C/m giúp e với ạ, giải 1 phần nhỏ trong bài th cũng đc ạ, e cảm ơn nhìu)Từ điểm A nằm ngoài đường tròn (O; R) với OA 2R. Vẽ tiếp tuyến AB và cát tuyến ACD với (O) (B là tiếp điểm; AC AD, tia AD không cắt đoạn thẳng OB). Gọi CE, DF là các đường cao của tam giác BCD. a) Chứng minh: tứ giác DEFC nội tiếp và EF//AB.b) Tia EF cắt AD tại G, BG cắt (O) tại H. Chứng minh: tam giác FHC đồng dạng tam giác GABc) Gọi I là giao điểm của CE và DF. Tia HI cắt DC tại M. Chứng minh: OM vuông góc với...
Đọc tiếp
C/m giúp e với ạ, giải 1 phần nhỏ trong bài th cũng đc ạ, e cảm ơn nhìu)
Từ điểm A nằm ngoài đường tròn (O; R) với OA > 2R. Vẽ tiếp tuyến AB và cát tuyến ACD với (O) (B là tiếp điểm; AC < AD, tia AD không cắt đoạn thẳng OB). Gọi CE, DF là các đường cao của tam giác BCD.
a) Chứng minh: tứ giác DEFC nội tiếp và EF//AB.
b) Tia EF cắt AD tại G, BG cắt (O) tại H. Chứng minh: tam giác FHC đồng dạng tam giác GAB
c) Gọi I là giao điểm của CE và DF. Tia HI cắt DC tại M. Chứng minh: OM vuông góc với CD
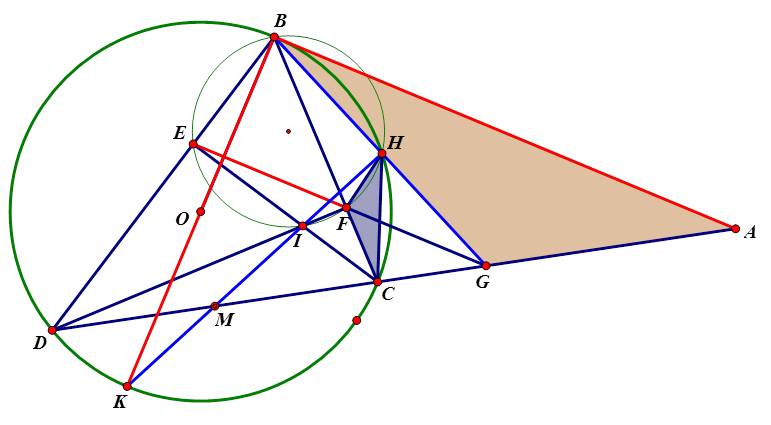
a: góc DEC=góc DFC=90 độ
=>DEFC nội tiếp
=>góc BFE=góc BDC=góc ABF
=>FE//AB
Đúng 1
Bình luận (0)
Cho điểm A ở ngoài đường tròn (O ;R). Kẻ hai tiếp tuyến AT, AT' và cát tuyến ABC với (O ;R). gọi H là trung điểm của BC ; TT' cắt OA và BC lần lượt tại I và J. a) Chứng minh : AT² = AI. AO b) Chứng minh các tam giác AIJ và AHO đồng dạng. Từ đó suy ra tích AJ. AH có giá trị không đổi khi cát tuyến ABC quay quanh A. c) Xác định vị trí điểm A để góc TAT'= 60°.
a: Xét (O) có
AT là tiếp tuyến
AT' là tiếp tuyến
Do đó: AT=AT'
hay A nằm trên đường trung trực của TT'(1)
Ta có: OT=OT'
nên O nằm trên đường trung trực của TT'(2)
Từ (1) và (2) suy ra AO là đường trung trực của TT'
Xét ΔOTA vuông tại T có TI là đường cao
nên \(AT^2=AI\cdot AO\)
b: Xét ΔAIJ vuông tại I và ΔAHO vuông tại H có
\(\widehat{HAO}\) chung
Do đó: ΔAIJ\(\sim\)ΔAHO
Đúng 0
Bình luận (1)
Cho (O),M là 1 điểm nằm ngoài (O).Vẽ tiếp tuyến MN và cát tuyến MBC.
a.Chứng minh rằng MN^2 = MB . MC
b.Vẽ cát tuyến MDE.Chứng minh rằng MB.MC = MD.ME


















