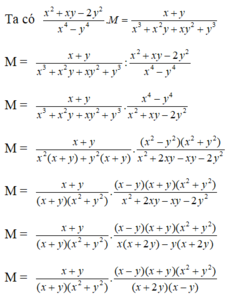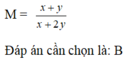TÌM M BIẾT:(25x2y-13xy2+y3)-m=11x2y-2y3

Những câu hỏi liên quan
Tìm đa thức A biết :A-(25x2y-10xy2+y3)=12x2y-2y3
\(A=12x^2y-2y^3+25x^2y-10xy^2+y^3=37x^2y-10xy^2-y^3\)
Đúng 1
Bình luận (0)
\(A=\left(12x^2y-2y^3\right)+\left(25x^2y-10xy^2+y^3\right)\)
\(A=37x^2y-10xy^2-y^3\)
Đúng 2
Bình luận (0)
Cho
(
25
x
2
y
-
10
x
y
2
+
y
3
)
-
A
12
x
2
y
-
2
y
3
. Đa thức A là: A.
A...
Đọc tiếp
Cho ( 25 x 2 y - 10 x y 2 + y 3 ) - A = 12 x 2 y - 2 y 3 . Đa thức A là:
A. A = 13 x 2 y + 3 y 3 + 10 x y 2
B. A = 13 x 2 y + 3 y 3 - 10 x y 2
C. A = 3 x 2 y + 3 y 3
D. A = 13 x 2 y - 3 y 3 - 10 x y 2
Ta có:
M − 3 x y − 4 y 2 = x 2 − 7 x y + 8 y 2 ⇒ M = x 2 − 7 x y + 8 y 2 + 3 x y − 4 y 2 ⇒ M = x 2 + ( − 7 x y + 3 x y ) + 8 y 2 − 4 y 2 ⇒ A = 13 x 2 y + 3 y 3 − 10 x y 2
Chọn đáp án B
Đúng 0
Bình luận (0)
Thu gọn đa thức
x
2
+
2
x
y
-
3
x
3
+
2
y
3
+
3
x
3
-
y
3
ta được đa thức A.
-
x
3
+
x
2...
Đọc tiếp
Thu gọn đa thức x 2 + 2 x y - 3 x 3 + 2 y 3 + 3 x 3 - y 3 ta được đa thức
A. - x 3 + x 2 + 2 x y + y 3
B. x 3 + x 2 + 2 x y + y 3
C. x 2 + 2 x y + y 3
D. x 2 + 2 x y - y 3
Chọn C
Ta có x2 + 2xy - 3x3 + 2y3 + 3x3-y3 = x2 + 2xy + y3.
Đúng 0
Bình luận (0)
Tính giá trị của mỗi đa thức sau:
x2 + 2xy – 3x3 + 2y3 + 3x3 – y3 tại x = 5 và y = 4
Gọi A = x2 + 2xy – 3x3 + 2y3 + 3x3 – y3
Trước hết ta thu gọn đa thức :
A = x2 + 2xy – 3x3 + 2y3 + 3x3 – y3
= (– 3x3+ 3x3) + x2 + 2xy + (2y3– y3)
= 0 + x2 + 2xy + y3.
= x2 + 2xy + y3.
Thay x = 5 ; y = 4 vào A ta được :
A = 52+ 2.5.4 + 43 = 25 + 40 + 64 = 129.
Vậy giá trị biểu thức x2 + 2xy – 3x3 + 2y3 + 3x3 – y3 tại x = 5 ; y = 4 bằng 129.
Đúng 0
Bình luận (0)
Cho các số thực dương x,y thỏa mãn xy+x+1 = 3y. Chứng minh rằng x3.y3+1≥2y3
\(xy+x+1=3y\Rightarrow x+\dfrac{1}{y}+\dfrac{x}{y}=3\)
Ta có:
\(x^3+1+1\ge3x\)
\(\dfrac{1}{y^3}+1+1\ge\dfrac{3}{y}\)
\(x^3+\dfrac{1}{y^3}+1\ge\dfrac{3x}{y}\)
Cộng vế:
\(2\left(x^3+\dfrac{1}{y^3}\right)+5\ge3\left(x+\dfrac{1}{y}+\dfrac{x}{y}\right)=9\)
\(\Rightarrow x^3+\dfrac{1}{y^3}\ge2\)
\(\Rightarrow x^3y^3+1\ge2y^3\) (đpcm)
Dấu "=" xảy ra khi \(x=y=1\)
Đúng 2
Bình luận (0)
Tìm biểu thức M, biết
x
2
+
x
y
−
2
y
2
x
4
−
y
4
.
M
x
+
y...
Đọc tiếp
Tìm biểu thức M, biết x 2 + x y − 2 y 2 x 4 − y 4 . M = x + y x 3 + x 2 y + x y 2 + y 3
A. x + y x − 2 y
B. x + y x + 2 y
C. x + y 2 x + y
D. x − y x + 2 y
1. Tính:a) 3x2y + (-4)x2y + 6x2yb) (-7)xy + (-dfrac{1}{2}) + 10xyc) 12xyz + 8xyz + (-5)xyz2. Tính giá trị của biểu thức:a) A x2 + 2xy - 3x3 + 2y3 + 3x3 - y3 tại x 5 và y 4b) B xy - x2y2 + x4y4 - x6y6 + x8y8 tại x -1 và y -13. Tìm đa thức C, biết: Ax2 - 2y + xy + 1 Bx2 + y - x2y2 - 1a) C A + Bb) C + A B
Đọc tiếp
1. Tính:
a) 3x2y + (-4)x2y + 6x2y
b) (-7)xy + (\(-\dfrac{1}{2}\)) + 10xy
c) 12xyz + 8xyz + (-5)xyz
2. Tính giá trị của biểu thức:
a) A= x2 + 2xy - 3x3 + 2y3 + 3x3 - y3 tại x= 5 và y= 4
b) B= xy - x2y2 + x4y4 - x6y6 + x8y8 tại x= -1 và y= -1
3. Tìm đa thức C, biết: A=x2 - 2y + xy + 1
B=x2 + y - x2y2 - 1
a) C= A + B
b) C + A = B
Bài 3:
a: Ta có: C=A+B
\(=x^2-2y+xy+1+x^2+y-x^2y^2-1\)
\(=2x^2-y+xy-x^2y^2\)
b: Ta có: C+A=B
\(\Leftrightarrow C=B-A\)
\(=x^2+y-x^2y^2-1-x^2+2y-xy-1\)
\(=-x^2y^2+3y-xy-2\)
Đúng 1
Bình luận (0)
Tính giá trị của biểu thức:
a) A= x2 + 2xy - 3x3 + 2y3 + 3x3 - y3 tại x= 5 và y= 4
b) B= xy - x2y2 + x4y4 - x6y6 + x8y8 tại x= -1 và y= -1
a) thay x=4 và y=5 vào biểu thức ta đc :129
b) tương tự....To be continued
Đúng 0
Bình luận (0)
a:\(A=x^2+2xy-3x^3+2y^3+3x^3-y^3\)
\(=x^2+2xy+y^3\)
\(=5^2+2\cdot5\cdot4+4^3\)
\(=25+40+64=129\)
Đúng 0
Bình luận (0)
M= (x+y).x2-y3. ( x+y)+(x2-y3)+3 biết x+y+1=0
Tìm x,y biết
25x2y \(⋮\)2;5 và chia 9 dư 1