Cho góc nhọn α, tính giá trị lớn nhất của P = 2sinα + 3cosα

Những câu hỏi liên quan
Cho góc α thỏa mãn: 3cosα+ 2sinα 2 và sinα 0. Tính sinα
Đọc tiếp
Cho góc α thỏa mãn: 3cosα+ 2sinα = 2 và sinα < 0. Tính sinα
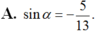



Chọn A.
Ta có 3cosα+ 2sinα = 2 hay (3cosα+ 2sinα = 2 )2 = 4
Tương đương: 9 cos2 α + 12 cosα .sin α + 4sin2α = 4
Hay 5cos2α + 12 cosα .sin α = 0
Từ đó: cosα= 0 hoặc 5cosα + 12 sinα = 0
+ Nếu cosα = 0 thì sinα =1: loại ( vì sinα < 0).
+ 5cosα + 12 sinα = 0
ta có hệ phương trình 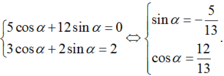
Đúng 0
Bình luận (0)
Tính các giá trị lượng giác của góc α, biết
cosα = 2sinα khi 0 < α < π/2
Với 0 < α < π/2 thì cosα >0, sinα >0. Ta có
1 - sin 2 α = cos 2 α
Mặt khác cos 2 α = ( 2 sin α ) 2 = 4 sin 2 α nên 5 sin 2 α = 1 hay
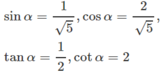
Đúng 0
Bình luận (0)
Cho tan
α
2. Tính giá trị của biểu thức:
G
2
sin
α
+
cos
α
cos
α
−
3
sin
α
A. G 1 B. G
−
4
5
C. G
−
6
5...
Đọc tiếp
Cho tan α = 2. Tính giá trị của biểu thức: G = 2 sin α + cos α cos α − 3 sin α
A. G = 1
B. G = − 4 5
C. G = − 6 5
D. G = −1
Vì tan α = 2 nên cos α ≠ 0
Ta có: G = 2 sin α + cos α cos α − 3 sin α = 2 sin α cos α + cos α sin α cos α cos α − 3 sin α cos α = 2 tan α + 1 1 − 3 tan α
Thay tan α = 2 ta được: G = 2.2 + 1 1 − 3.2 = − 5 5 = − 1
Vậy G = −1
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
với α là góc nhọn tim giá trị lớn nhất của biểu thức sinα +sin (90 0 - α )
Đặt \(A=sin\alpha+sin\left(90^0-\alpha\right)=sin\alpha+cos\alpha\)
\(\Rightarrow A^2=\left(sin\alpha+cos\alpha\right)^2\le2\left(sin^2\alpha+cos^2\alpha\right)=2\)
\(\Rightarrow A\le\sqrt{2}\)
\(A_{max}=\sqrt{2}\) khi \(\alpha=45^0\)
Đúng 4
Bình luận (0)
Cho biết 3cosα – sinα = 1; 00 < α < 900. Giá trị của tanα bằng:
A. 4/3
B. 3/4
C. 1
D. ½
Chọn A.
Ta có 3cosα – sinα = 1 nên 3cosα = sinα + 1
Suy ra: 9cos2α = sin2α + 2sinα + 1
Hay 10sin2α + 2sinα - 8 = 0
Do đó: sinα = -1 hoặc sinα = 0,8
+ sinα = -1 không thỏa mãn vì 00 < α < 900
+ sinα = 0,8 thì cosα = 0,6 và tan α = 0,8 : 0,6 = 4/3.
Đúng 0
Bình luận (0)
Cho biết
3
cos
α
−
sin
α
1
,
0
0
α
90
0
.
Giá trị của
tan
α
bằng A.
tan
α
4
3
.
B.
tan
α
3
4
.
C.
tan
α...
Đọc tiếp
Cho biết 3 cos α − sin α = 1 , 0 0 < α < 90 0 . Giá trị của tan α bằng
A. tan α = 4 3 .
B. tan α = 3 4 .
C. tan α = 4 5 .
D. tan α = 5 4 .
Ta có 3 cos α − sin α = 1 ⇔ 3 cos α = sin α + 1 → 9 cos 2 α = sin α + 1 2
⇔ 9 cos 2 α = sin 2 α + 2 sin α + 1 ⇔ 9 1 − sin 2 α = sin 2 α + 2 sin α + 1
⇔ 10 sin 2 α + 2 sin α − 8 = 0 ⇔ sin α = − 1 sin α = 4 5 .
sin α = − 1 : không thỏa mãn vì 0 0 < α < 90 0 .
sin α = 4 5 ⇒ cos α = 3 5 ⇒ tan α = sin α cos α = 4 3 .
Chọn A.
Đúng 0
Bình luận (0)
Cho biết
3
cos
α
−
sin
α
1
,
0
0
α
90
0
.
Giá trị của
tan
α
bằng A.
tan
α
4
3
.
B.
tan
α
3
4
.
C.
tan
α
4
5...
Đọc tiếp
Cho biết 3 cos α − sin α = 1 , 0 0 < α < 90 0 . Giá trị của tan α bằng
A. tan α = 4 3 .
B. tan α = 3 4 .
C. tan α = 4 5 .
D. tan α = 5 4 .
Cho biết
3
cos
α
−
sin
α
1
,
0
0
α
90
0
.
Giá trị của tanα bằng A.
tan
α
4
3
.
B.
tan
α
3
4
.
...
Đọc tiếp
Cho biết 3 cos α − sin α = 1 , 0 0 < α < 90 0 . Giá trị của tanα bằng
A. tan α = 4 3 .
B. tan α = 3 4 .
C. tan α = 4 5 .
D. tan α = 5 4 .
Ta có:
3 cos α − sin α = 1 ⇔ 3 cos α = sin α + 1 → 9 cos 2 α = sin α + 1 2
⇔ 9 cos 2 α = sin 2 α + 2 sin α + 1 ⇔ 9 1 − sin 2 α = sin 2 α + 2 sin α + 1
⇔ 10 sin 2 α + 2 sin α − 8 = 0 ⇔ sin α = − 1 sin α = 4 5 .
sin α = − 1 : không thỏa mãn vì 0 0 < α < 90 0 .
sin α = 4 5 ⇒ cos α = 3 5 ⇒ tan α = sin α cos α = 4 3 .
Chọn A.
Đúng 0
Bình luận (0)
Cho góc nhọn α. Giá trị của biểu thức
P
s
i
n
2
90
°
−
α
+
s
i
n
2
α
là A.1 B. 2 C.
2
s
i
n
2
90
°
−
α
D.
2
s
i
n...
Đọc tiếp
Cho góc nhọn α. Giá trị của biểu thức P = s i n 2 90 ° − α + s i n 2 α là
A.1
B. 2
C. 2 s i n 2 90 ° − α
D. 2 s i n 2 α
Đáp án A
P = s i n 2 90 ° − α + s i n 2 α = c o s 2 α + s i n 2 α = 1
Đúng 0
Bình luận (0)






