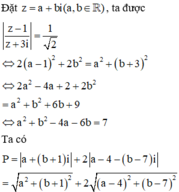CHO BIỂU THỨC I X-7I+IY-8I+I Z-(-9) I= 0 TÍNH TỔNG X+Y+Z

Những câu hỏi liên quan
1) Cho biểu thức: Pleft(dfrac{9}{x^3-9x}+dfrac{1}{x+3}right):left(dfrac{x-3}{x^3+3x}-dfrac{x}{3x+9}right)
a. Nêu điều kiện xác định và rút gọn biểu thức P
b. Tìm x để |P| 2
c. Với x 3. Tìm GTNN của biểu thức MPcdotdfrac{x^2+2x+10}{-3}
2) Cho x, y, z thỏa mãn:
dfrac{19}{x+y}+dfrac{19}{y+z}+dfrac{19}{z+x}dfrac{7x}{y+z}+dfrac{7z}{x+y}+dfrac{7y}{x+z}dfrac{133}{10}Tính giá trị biểu thức M x + y + z.
Đọc tiếp
1) Cho biểu thức: \(P=\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^3+3x}-\dfrac{x}{3x+9}\right)\)
a. Nêu điều kiện xác định và rút gọn biểu thức P
b. Tìm x để |P| = 2
c. Với x > 3. Tìm GTNN của biểu thức \(M=P\cdot\dfrac{x^2+2x+10}{-3}\)
2) Cho x, y, z thỏa mãn:
\(\dfrac{19}{x+y}+\dfrac{19}{y+z}+\dfrac{19}{z+x}=\dfrac{7x}{y+z}+\dfrac{7z}{x+y}+\dfrac{7y}{x+z}=\dfrac{133}{10}\)Tính giá trị biểu thức M = x + y + z.
Cho số phức zx+iy (x,y∈R) thỏa mãn
2
z
+
(
1
+
i
-
i
3
)
z
x
+
2
+
3
i
. Trên mặt p...
Đọc tiếp
Cho số phức z=x+iy (x,y∈R) thỏa mãn 2 z + ( 1 + i - i 3 ) z = x + 2 + 3 i . Trên mặt phẳng tọa độ, điểm biểu diễn số phức z có tọa độ là
A. (2;-3).
B. (-1;2).
C. (2;1).
D. (2;-1).
1. Tính giá trị của biểu thức
\(M=\left(x+y\right)\left(y+z\right)\left(x+z\right)\) với \(x+y+z=0\)
2. Tìm \(x,y,z,t\) biết rằng :
a. \(yt=48;yz=24;xy=12;zt=32\)
b. \(y+t=11;y+z=9;x+y=6;z+t=12\)
\(1.\)
Ta có :
\(x+y+z=0\)
\(\Rightarrow x+y=-z\)
\(y+z=-x\)
\(x+z=-y\)
\(\Rightarrow M=\left(-z\right)\left(-x\right)\left(-y\right)=-xyz\)
Mà \(xyz=2\)
\(\Rightarrow M=-2\)
Vậy : \(M=-2\)
Đúng 0
Bình luận (0)
\(2.\)
\(a.\)
Ta có :
\(yt.yz=48.24\)
\(\Rightarrow y^2.zt=48.24\)
Mà \(yt=32\Rightarrow y^2.32=48.24\)
\(\Rightarrow y^2=\frac{48.24}{32}\)
\(\Rightarrow y^2=36\)
\(\Rightarrow y=\pm6\)
+ Nếu \(x=6\)
Ta có : \(t=48:6=8\)
\(z=24:6=4\)
\(x=12:6=2\)
+ Nếu \(y=-6\)
Ta có : \(t=48:\left(-6\right)=-8\)
\(z=24:\left(-6\right)=-4\)
\(x=12:\left(-6\right)=-2\)
Vậy \(x=-2;y=-6;z=-4;t=-8\) hoặc \(x=2;y=6;z=4;t=8\)
\(b.\)
Ta có :
\(y+t=11\) \(\left(1\right)\)
\(y+z=9\) \(\left(2\right)\)
\(x+y=6\) \(\left(3\right)\)
\(z+t=12\) \(\left(4\right)\)
Lấy \(\left(1\right)+\left(2\right)\), ta được :
\(2y+t+z=20\)
Mà \(t+z=12\)
\(\Rightarrow2y+12=20\)
\(\Rightarrow2y=8\)
\(\Rightarrow y=4\)
Từ \(\left(2\right)\) \(\Rightarrow z=9-y=9-4=5\)
Từ \(\left(3\right)\) \(\Rightarrow x=6-y=6-4=2\)
Từ \(\left(4\right)\) \(\Rightarrow t=12-z=12-5=7\)
Vậy : \(x=2;y=4;z=5;t=7\)
Đúng 0
Bình luận (0)
Mình ghi lộn câu 1
\(M=\left(x+y\right)\left(y+z\right)\left(x+z\right)\) biết \(xyz=2\) và \(x+y+z=0\)
Đúng 0
Bình luận (0)
Cho biểu thức A = \(|2x-3y|+|2y+3z|+|x+y+\dfrac{x}{z}|\) với z\(\ne\)0 Tìm x,y,z để A có giá trị bằng 0
giúp tui i đg cần gấp ;-;
=>2x-3y=0 và 2y+3z=0 và x+y+x/z=0
=>x/3=y/2 và y/-3=z/2 và x+y+x/z=0
=>x/9=y/6=z/-4 và x+y+x/z=0
x/9=y/6=z/-4=k
=>x=9k; y=6k; z=-4k
x+y+x/z=0
=>9k+6k+9k/-4k=0
=>15k=9/4
=>k=9/60=3/20
=>x=27/20; y=9/10; z=-3/5
Đúng 0
Bình luận (0)
Tính tổng x và y sao cho:
I x - 30 I + Iy + ̀50 I = 0
/x-30/ >/ 0;/y+50/ >/ 0
=>/x-30/+/y+50/ >/ 0
Theo đề:/x-30/+/y+50/=0
=>x-30=y+50=0
=>x=30;y=-50
=>x+y=-20
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
-
1
z
+
3
i
1
2
.
Tìm giá trị lớn nhất của biểu thức
P
z
+
i
+
2
z...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 z + 3 i = 1 2 . Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z ¯ - 4 + 7 i
A. 10
B. 20
C. 2 5
D. 4 5
Cho số phức z thỏa mãn
z
−
1
z
+
3
i
1
2
.
Tìm giá trị lớn nhất của biểu thức
P
z
+
i
+
2
z...
Đọc tiếp
Cho số phức z thỏa mãn z − 1 z + 3 i = 1 2 .
Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z ¯ − 4 + 7 i
A. 8
B. 10
C. 2 5
D. 4 5
Đáp án B
Đặt z = x + y i x , y ∈ ℝ , khi đó z − 1 z + 3 i = 1 2 ⇔ 2 z − 1 = z + 3 i
⇔ 2 x − 1 2 + y 2 = x 2 + y + 3 2 ⇔ x − 2 2 + y − 3 2 = 20 C
Suy ra tập hợp điểm biểu diễn số phức z là đường tròn (C), tâm I 2 ; 3 , bán kính R = 2 5
Ta có P = z + i + 2 z ¯ − 4 + 7 i = z + i + 2 z − 4 + 7 i , với A 0 ; − 1 , B 4 ; 7 ⇒ P = M A + 2 M B
Vậy P = M A + 2 M B ≤ 1 2 + 2 2 M A 2 + M B 2 = 5.20 = 10 → P m a x = 10
Đúng 0
Bình luận (0)
Cho số phức z thõa mãn
z
-
1
z
+
3
i
1
2
. Tìm giá trị lớn nhất của biểu thức
P
z
+
i
+
2
z
¯...
Đọc tiếp
Cho số phức z thõa mãn z - 1 z + 3 i = 1 2 . Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z ¯ - 4 + 7 i
A. 8
B. 20
C. 2 5
D. 4 5
Cho số phức z thỏa mãn
z
-
1
z
+
3
i
1
2
. Tìm giá trị lớn nhất của biểu thức
P
z
+...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 z + 3 i = 1 2 .
Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z ¯ - 4 + 7 i .
A. 10
B. 20
C. 2 5
D. 4 5
Đáp án B
Ta có 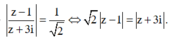
Gọi M là điểm biểu diễn số phức, tập hợp điểm biểu diễn số phức z là đường tròn có phương trình
![]()
![]()
A(0;-1), B(4;7) lần lượt biểu diễn 2 số phức ![]()
Ta có ![]() nên AB là bán kính đường tròn (C)
nên AB là bán kính đường tròn (C)
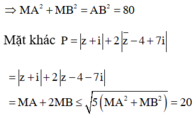
Dấu “=” xảy ra khi MB=2MA
Vậy maxP= 20
Đúng 0
Bình luận (0)