biết phương trình -x2 +22021x+1=0 có 2 nghiệm .tính tổng 2 nghiệm đó

Những câu hỏi liên quan
Cho phương trình bậc 2: (m - 1)x2 - 2mx + m + 1 = 0.
a) Tìm m, biết phương trình có nghiệm x = 0.
b) Xác định giá trị của m để phương trình có tích 2 nghiệm bằng 5, từ đó hãy tính tổng 2 nghiệm của phương trình.
a) Thay \(x=0\) vào phương trình ta có:
\(\left(m-1\right).0^2-2m.0+m+1=0.\\ \Leftrightarrow m+1=0.\\ \Leftrightarrow m=-1.\)
b) Ta có: \(\Delta'=m^2-\left(m-1\right)\left(m+1\right).\)
\(\Delta'=m^2-\left(m^2-1\right).\\ =m^2-m^2+1.\\ =1>0.\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt \(x_1;x_2.\)
Theo Viet: \(\left\{{}\begin{matrix}x_1.x_2=\dfrac{m+1}{m-1}.\\x_1+x_2=\dfrac{2m}{m-1}.\left(1\right)\end{matrix}\right.\)
Theo đề bài: \(x_1.x_2=5.\)
\(\Rightarrow\dfrac{m+1}{m-1}=5.\\ \Leftrightarrow m+1=5m-5.\\ \Leftrightarrow4m-6=0.\\ \Leftrightarrow m=\dfrac{3}{2}.\)
Thay \(m=\dfrac{3}{2}\) vào \(\left(1\right):\)
\(x_1+x_2=\) \(\dfrac{2.\dfrac{3}{2}}{\dfrac{3}{2}-1}=\dfrac{3}{\dfrac{1}{2}}=6.\)
Đúng 1
Bình luận (0)
Câu 3: Phương trình : 2013x2 – 2015x + 2 0 có 2 nghiệm là:A. x1 -1 và x2 -2/2013 B. x1 1 và x2 2/2013C. Phương trình vô nghiệm D. Cả ba đáp án trên đều sai.Câu 4: Cho phương trình x2 + 3x + 1 0, khi đó tổng các nghiệm bằng A. 3 B. - 3 C. 1 D. -1 Câu 5: Phương trình nào sau đây vô nghiệm: A. 4x2 - 5x + 1 0 B. 2x2 + x – 1 0 C. 3x2 + x + 2 0 D. x2 + x – 1...
Đọc tiếp
Câu 3: Phương trình : 2013x2 – 2015x + 2 = 0 có 2 nghiệm là:
A. x1 = -1 và x2 = -2/2013 B. x1 = 1 và x2 = 2/2013
C. Phương trình vô nghiệm D. Cả ba đáp án trên đều sai.
Câu 4: Cho phương trình x2 + 3x + 1 = 0, khi đó tổng các nghiệm bằng
A. 3 B. - 3 C. 1 D. -1
Câu 5: Phương trình nào sau đây vô nghiệm:
A. 4x2 - 5x + 1 = 0 B. 2x2 + x – 1 = 0 C. 3x2 + x + 2 = 0 D. x2 + x – 1 = 0
Câu 6: Phương trình x2 - 7x + 6 = 0,khi đó tích các nghiệm bằng
A. -7 B. 6 C. - 6 D. 7
Câu 3:
$\Delta=2015^2-4.2013.2=2011^2$
Do đó pt có 2 nghiệm:
$x_1=\frac{2015+2011}{2.2013}=1$
$x_2=\frac{2015-2011}{2.2013}=\frac{2}{2013}$
Đáp án B.
Đúng 2
Bình luận (0)
Câu 4:
Theo định lý Viet, tổng các nghiệm của pt là:
$S=\frac{-b}{a}=\frac{-3}{1}=-3$
Đáp án B.
Đúng 2
Bình luận (0)
Câu 5:
PT (C) có $\Delta'=1-4.3.2<0$ nên PT này vô nghiệm
Đáp án C.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Biết rằng phương trình
l
o
g
2
3
x
-
(
m
+
2
)
l
o
g
3
x
+
3
m
-
1
0
có hai nghiệm
x
1
,
x
2
thảo mãn
x
1...
Đọc tiếp
Biết rằng phương trình l o g 2 3 x - ( m + 2 ) l o g 3 x + 3 m - 1 = 0 có hai nghiệm x 1 , x 2 thảo mãn x 1 . x 2 = 27 . Khi đó tổng x 1 + x 2 bằng
A. 6
B. 12
C. 1 3
D. 34 3
Phương trình
3.9
x
−
10.3
x
+
3
0
có 2 nghiệm
x
1
,
x
2
.
Khi đó tổng 2 nghiệm A.
x
1
+
x
2
1
3
B.
x...
Đọc tiếp
Phương trình 3.9 x − 10.3 x + 3 = 0 có 2 nghiệm x 1 , x 2 . Khi đó tổng 2 nghiệm
A. x 1 + x 2 = 1 3
B. x 1 + x 2 = − 1
C. x 1 + x 2 = 10 3
D. x 1 + x 2 = 0
Đáp án D
Ta có 3.9 x − 10.3 x + 3 = 0 ⇔ 3. 3 x 2 − 10.3 x + 3 = 0 ⇔ 3 x = 3 3 x = 1 3 ⇔ x = 1 x = − 1
Đúng 0
Bình luận (0)
Cho phương trình (2m - 1)
x
2
- 2(m + 4)x + 5m + 2 0 ( m
≠
1
2
)Khi phương trình có nghiệm
x
1
,
x
2
hãy tính tổng S và tích P của hai nghiệm theo m
Đọc tiếp
Cho phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
Khi phương trình có nghiệm x 1 , x 2 hãy tính tổng S và tích P của hai nghiệm theo m
Phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
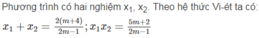
Đúng 0
Bình luận (0)
Cho phương trình bậc hai : x2 + 2m + m +6 0 (6).a/ Tìm m để phương trình (6) có nghiệm x -1. ? Tính nghiệm còn lại. b/ Tìm m để phương trình (6) có nghiệm kép? Tính nghiệm kép đó. c/ Gọi x1, x2 là 2 nghiệm của phương trình (6). Tìm m để A x1 +x2 -x1.x2 đạt giá trị lớn nhất
Đọc tiếp
Cho phương trình bậc hai : x2 + 2m + m +6 = 0 (6).
a/ Tìm m để phương trình (6) có nghiệm x = -1. ? Tính nghiệm còn lại.
b/ Tìm m để phương trình (6) có nghiệm kép? Tính nghiệm kép đó.
c/ Gọi x1, x2 là 2 nghiệm của phương trình (6). Tìm m để A = x1 +x2 -x1.x2 đạt giá trị lớn nhất
a: Thay x=-1 vào (6), ta được:
1+2m+m+6=0
=>3m+7=0
=>m=-7/3
x1+x2=-2m/1=-2*7/3=-14/3
=>x2=-14/3-x1=-14/3+1=-11/3
b: \(\text{Δ}=0^2-2\left(2m+m+6\right)=-2\left(3m+6\right)\)
Để phương trình có nghiệm kép thì 3m+6=0
=>m=-2
Khi m=-2 thì (6) sẽ là x^2+2*(-2)-2+6=0
=>x^2-4x+4=0
=>x=2
Đúng 0
Bình luận (1)
Cho phương trình
x2+mx+2m-4=0
a Chứng tỏ phương trình trên luôn có nghiệm với mọi giá trị m
b Tính tổng và tích của 2 nghiệm theo m
c Tìm m để phương trình có 2 nghiệm x1,x2 thỏa mãn x1^2+x2^2=4 
a.
\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0;\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=2m-4\end{matrix}\right.\)
c.
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow m^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+4=0\Rightarrow m=2\)
Đúng 3
Bình luận (0)
a.\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0\)
=> pt luôn có nghiệm với mọi m
b.Theo hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1.x_2=2m-4\end{matrix}\right.\)
c.\(x_1^2+x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=4\)
\(\Leftrightarrow\left(-m\right)^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+8-4=0\)
\(\Leftrightarrow m^2-4m+4=0\)
\(\Leftrightarrow\left(m-2\right)^2=0\)
\(\Leftrightarrow m=2\)
Đúng 2
Bình luận (0)
Cho phương trình
(
m
+
1
)
x
2
+
(
3
m
-
1
)
x
+
2
m
-
2
0
. Xác định m để phương trình có hai nghiệm
x
1
,
...
Đọc tiếp
Cho phương trình ( m + 1 ) x 2 + ( 3 m - 1 ) x + 2 m - 2 = 0 . Xác định m để phương trình có hai nghiệm x 1 , x 2 mà x 1 + x 2 = 3 . Tính các nghiệm trong trường hợp đó.
Với m ≠ -1
Ta có: Δ = ( m - 3 ) 2 ≥ 0 , do đó phương trình luôn luôn có hai nghiệm x 1 , x 2
Lúc đó phương trình đã cho có hai nghiệm x = -1 và x = 4.
Đúng 0
Bình luận (0)
cho phương trình (m-1)x2 -2mx +m+1 =0
a) tìm m biết phương trình có nghiệm x=0
b) xác định giá trị của m để phương trình có tích 2 nghiệm bằng 5 từ đó hãy tính tổng 2 nghiệm của phương trình
a) x = 0 là nghiệm của phương trình
=> (m-1).02 -2.m.0 + m + 1 = 0
<=> m + 1 = 0 <=> m = -1
vậy m = -1 thì pt có nghiệm là x = 0
b) PT có 2 nghiệm thì trước hết pt đã cho là phương trình bậc 2 <=> m - 1\(\ne\) 0 <=> m \(\ne\)1
\(\Delta\)' = (-m)2 - (m - 1)(m +1) = m2 - (m2 - 1) = 1 > 0
=> phương trình đã cho có 2 nghiệm là:
x1 = \(\frac{m+1}{m-1}\) ; x2 = \(\frac{m-1}{m-1}\) = 1
+) Để x1 .x2 = 5 <=> \(\frac{m+1}{m-1}\) = 5 <=> m +1 = 5( m - 1)
<=> m +1 = 5m - 5
<=> 6 = 4m <=> m = 3/2 (Thoả mãn)
+) Khi đó x1 + x2 = \(\frac{m+1}{m-1}\) + 1 = \(\frac{m+1+m-1}{m-1}=\frac{2m}{m-1}=\frac{2.\frac{3}{2}}{\frac{3}{2}-1}=\frac{3}{\frac{1}{2}}=6\)
Đúng 1
Bình luận (0)
Mình không đồng ý với phần tìm đen-ta của bạn Trần Thị Loan
Phương trình (m-1)x2 - 2mx + m + 1 = 0 ( a=m-1; b=-2m; c=m+1)
đen-ta = (-2m)2 - 4.(m-1).(m=1)=4
Vì đen-ta = 4 > 0 nên phương trình có 2 nghiệm phân biệt với mọi m
Phần b) còn cách 2 ngắn hơn như sau :
Để (m-1)x2 - 2mx + m + 1 = 0 thì m-1\(\ne\)0 \(\Leftrightarrow m\ne1\)
Vì x1 và x2 là 2 nghiệm của phương trình nên áp dụng hệ thức Vi-ét ta có :
\(x_1.x_2=5\\ \Leftrightarrow\frac{m+1}{m-1}=5\\ \Leftrightarrow m+1=5.\left(m-1\right)\\ \Leftrightarrow m+1=5m-5\\ \Leftrightarrow-4m=-6\\ m=\frac{3}{2}\left(tmđk\right)\)
Vậy \(m=\frac{3}{2}\)thì phương trình có tích hai nghiệm bằng 5
\(x_1+x_2=\frac{m+1}{m-1}+1=\frac{m+1}{m-1}+\frac{m-1}{m-1}=\frac{m+1+m-1}{m-1}=\frac{2m}{m-1}\left(1\right)\)
Thay \(m=\frac{3}{2}\)vào (1) ta được :
\(\frac{2.\frac{3}{2}}{\frac{3}{2}-1}=\frac{3}{\frac{1}{2}}=6\)



















