Cần phải thiết kế các thùng dạng hình trụ có nắp đựng nước sạch có dung tích V c m 3 . Hỏi bán kính R c m của đáy hình trụ nhận giá trị nào sau đây để tiết kiệm vật liệu nhất?
A. R = 3 V 2 π 3
B. R = V π 3
C. R = V 4 π 3
D. R = V 2 π 3
Cần phải thiết kế các thùng dạng hình trụ có nắp đựng nước sạch có dung tích V ( c m 3 ). Hỏi bán kính R (cm) của đáy hình trụ nhận giá trị nào sau đây để tiết kiệm vật liệu nhất?
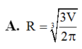
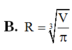
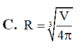
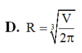
Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung tích là 20lít. Cần phải thiết kế thùng sơn đó với bán kính nắp đậy là bao nhiêu (cm) để nhà sản xuất tiết kiện được vật liệu nhất?
A. 100 π 3
B. 10000 π 3
C. 200 π
D. 200 π
Đáp án B
Đổi 20 lít =20000cm3.
Gọi bán kính nắp đậy của thùng sơn là x (cm), x>3,
chiều cao của thùng sơn là h(cm).
Khi đó thể tích của thùng sơn là

giúp mình vs ạ
Người ta thiết kế 1 thùng tôn hình trụ không có nắp để đựng nước có dung tích bằng 2 mết khối. chiều cao thủng là 2m. Hỏi phải dung ối thiểu bao nhiêu mét vuông tôn để làm được chiếc thùng trên.
Lời giải:
Diện tích đáy: $2:2=1$ (m2)
Bán kính đáy: $\sqrt{1:3,14}=0,56$ (m)
Chu vi đáy: $0,56.2.3,14=3,5$ (m)
Diện tích làm tôn:
$3,5.2+1=8$ (m2)
giúp mình vs ạ
Người ta thiết kế 1 thùng tôn hình trụ không có nắp để đựng nước có dung tích bằng 2 mết khối. chiều cao thủng là 2m. Hỏi phải dung ối thiểu bao nhiêu mét vuông tôn để làm được chiếc thùng trên.
Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dug tích là 20 lít. Cần phải thiết kế thùng sơn đó với bán kính nắp đậy là bao nhiêu (cm) để nhà sản xuất tiết kiệm được vật liệu nhất?
A. 200 π
B. 100 π 3
C. 1000 π 3
D. 200 π
Đáp án C
Đổi 20 lít = 20 000 cm3
Gọi bán kính nắp đậy của thùng sơn là x (cm), x > 0, chiều cao của thùng sơn là h (cm)
Khi đó thể tích của thùng sơn là
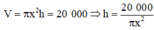
Diện tích toàn phần của thùng sơn là:
![]()
Để nhà sản xuất tiết kiệm được vật liệu nhất tức là Stp nhỏ nhất
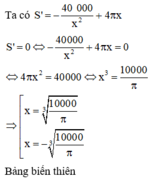
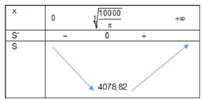
Vậy bán kính nắp đậy là 1000 π 3 thì sẽ tiết kiệm vật liệu nhất
Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dug tích là 20 lít. Cần phải thiết kế thùng sơn đó với bán kính nắp đậy là bao nhiêu (cm) để nhà sản xuất tiết kiệm được vật liệu nhất?
![]()
![]()
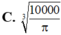
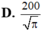
Người ta thiết kế một thùng tôn hình trụ không có nắp đựng nước có dung tích bằng 2m3 . Biết chiều cao thùng tôn là 2m , hỏi phải dùng tối thiểu bao nhiêu m3 tôn để làm được thùng tôn trên ? Lấy π=3,14 và kết quả làm tròn đến 2 chữ số thập phân
Lời giải:
Diện tích mặt đáy: $2:2=1$ (m2)
Bán kính đáy: $\sqrt{1:3,14}=0,56$ (m)
Chu vi đáy: $0,56.2.3,14=3,5$ (m)
Diện tích tôn làm thùng:
$3,5\times 2+ 1=8$ (m2)
một người thợ định làm 1 thùng để đựng 2m^3 nước dạng hình trụ (không nắp) để tiết kiệm vật liệu nhất cần làm đáy của thùng có bán kính
Một bồn nước inox được thiết kế có dạng hình trụ (có nắp) đựng được 10 mét khối nước. Tìm bán kính r của đáy bồn nước biết lượng inox được sử dụng để làm bồn nước là ít nhất?
A. r = 5 π 3 m
B. r = 5 π 3 m
C. r = 5 2 π 3 m
D. r = 10 π 3 m
Đáp án B.
Gọi h(m) là chiều cao của chiếc bồn nước, h > 0 .
Thể tích của chiếc bồn là V = π r 2 h = 10 ⇒ h = 10 π r 2 .
Diện tích toàn phần của chiếc bồn là:
S t p = 2 π r 2 + 2 π r h = 2 π r 2 + 2 π r . 10 π r 2 = 2 π r 2 + 20 r = 2 π r 2 + 10 r + 10 r
Cách 1: Theo bất đẳng thức Côsi ta có: S t p ≥ 3 2 π r 2 . 10 r . 10 r 3 = 3. 200 π 3 .
Dấu “=” xảy ra khi
2 π r 2 = 10 r ⇔ r 3 = 5 π ⇔ r = 5 π 3
Vậy với r = 5 π 3 thì lượng inox được sử dụng để làm bồn nước là ít nhất.
Cách 2: Xét hàm số f r = 2 π r 2 + 20 r , r > 0 .
Ta có
f ' r = 4 π r − 20 r 2 = 4 π r 3 − 20 r 2 ; f ' r = 0 ⇔ 4 π r 3 − 20 = 0 ⇔ r 3 = 5 π ⇔ r = 5 π 3
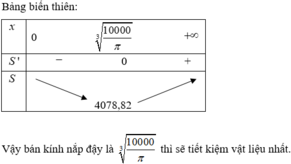
Bảng biến thiên:
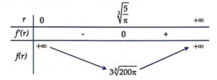
⇒ f r đạt giá trị nhỏ nhất tại r = 5 π 3 .