Gía trị lớn nhất của hàm số y = x 3 − 2 x 2 − 4 x + 5 trên đoạn [1;3] bằng
A. -3
B. 0
C. 2
D. 3
a )tìm giá trị lớn nhấy của hàm số y=-3/5 x nếu -5 <hoặc = x < hoặc = 2014
b) tìm số nguyên x để biểu thức A=4x-5 / 3x + 2 có giá trị lớn nhất. tìm gía trị lớn nhất đó
giúp mình vs các bạn ơi ai nhanh mình tích cho
Gía trị lớn nhất của hàm số y = - 2 4 - x là
A. -4
B. -2
C. 1
D. 0
1/Giá trị nhỏ nhất của C=(x^2+13)^2
2/Gía trị lớn nhất của B=-(x-3)^2+5/4
3/ Gía trị của x để A=|x-1/3| nhỏ nhất
4/ Tổng các giá trị x thỏa mãn 3x^2-50x=0
Tìm gía trị nhỏ nhất của hàm số - x + 3 - 1 x + 2 trên nửa khoảng [ - 4 ; - 2 )
A. m i n - 4 ; - 2 y = 4
B. m i n - 4 ; - 2 y = 5
C. m i n - 4 ; - 2 y = 15 2
D. m i n - 4 ; - 2 y = 7
Đáp án là D.
• Ta có: y , = - 1 - 1 ( 2 + x ) 2 cho y , = 0 ⇔ x = - 1 x = - 3
• Bảng biến thiên:
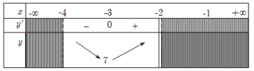
Từ BBT ta có: m i n - 4 ; - 2 y = 7
1)số nguyên x lớn nhất để -4 - x >3 là.....
2)Số cặp số (x;y)thỏa mãn (x^2 +2)(y^4+6)=10
3)Gía trị nguyên nhỏ nhất của n để A=5/n-7 nguyên để n=...
4)Tập hợp các số nguyên x sao cho x^2+4.x+5 là bội của x+4 là {....}
(nhập các giá trị theo thứ tự tăng dần )
5)Số các số tự nhiên có bốn chữ số chia 3 dư 1 và chia 5 dư 2 là....
6)Số cặp số nguyên (x;y) thỏa mãn (2x - 5 ) (y -6) = 17 là....
Một bài làm không được mà bạn ra 6 bài thì ............
1) -4 - x > 3 => -4 - 3 > x => -7 > x => số nguyên x lớn nhất = -8
2) Vì x2 + 2 \(\ge\) 2 ; y4 + 6 \(\ge\) 6 với mọi x; y => (x2 + 2). (y4 + 6) \(\ge\) 2.6 = 12 > 10
=> Không tồn tại x; y để thỏa mãn
3) A nguyên khi 5 chia hết cho n- 7 hay n - 7 là ước của 5
mà n nhỏ nhất nên n - 7 nhỏ nhất => n - 7 = -5 => n = 2
4) x2 + 4x + 5 = x(x+ 4) + 5 chia hết cho x + 4 => 5 chia hết cho x + 4
=> x + 4 \(\in\) {5;-5;1;-1} => x \(\in\) {1; -9; -3; -5}
5) Gọi số đó là n
n chia 3 dư 1 => n - 1 chia hết cho 3 => n - 1 + 9 = n + 8 chia hết cho 3
n chia cho 5 dư 2 => n - 2 chia hết cho 5 => n - 2 + 10 = n + 8 chia hết cho 5
=> n + 8 chia hết cho 3 và 5 => n + 8 chia hết cho 15 => n + 8 \(\in\) B(15)
Vì n có 4 chữ số nên n + 8 \(\in\) {68.15 ; 69.15 ; ...' ; 667.15}
=> có (667 - 68) : 1 + 1 = 600 số
6) (2x-5).(y-6) = 17 = 1.17 = 17.1 = (-1).(-17) = (-17).(-1)
=> có 4 cặp x; y thỏa mãn
Cho hàm số f (x) có đạo hàm là f ' x . Đồ thị hàm số y = f ' x được cho như hình bên. Biết rằng f 0 + f 3 = f 2 + f 5 . Gía trị nhỏ nhất, giá trị lớn nhất của f (x) trên đoạn 0 ; 5 lần lượt là
A. f 2 , f 5
B. f 0 , f 5
C. f 2 , f 0
D. f 1 , f 5
Đáp án A
Lập được bảng biến thiên của hàm số như sau:
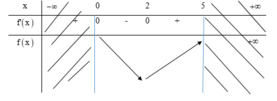
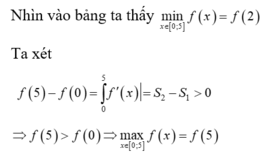
Tìm giá trị lớn nhất, giá trị lớn nhất của hàm số (nếu có)
a, \(y=\sqrt{x^2+x-2}\)
b, \(y=\sqrt{2+x}+\sqrt{4-x}\)
c, \(y=x+\sqrt{4-x^2}\)
Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$
Câu 1: Cho hàm số y = (3m + 5) x\(^2\) với m \(\ne\) \(\dfrac{-5}{3}\). Tìm các giá trị của tham số m để hàm số:
a) Nghịch biến với mọi x > 0
b) Đồng biến với mọi x >0
c) Đạt giá trị lớn nhất là 0
d) Đạt giá trị nhỏ nhất là 0
Câu 2: Cho hàm số y = \(\left(\sqrt{3k+4}-3\right)x^2\) với k \(\ge\dfrac{-4}{3}\); k \(\ne\dfrac{5}{3}\)
Tính các giá trị của tham số K để hàm số:
a) Nghịch biến với mọi x >0
b) Đồng biến với mọi x >0
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)
1) giá trị lớn nhất của hàm số \(y=-\sqrt{x-2}+\sqrt{4-x}\)
2)GTLN của hàm số \(y=\dfrac{1}{4}x^2-x-\sqrt{4x-x^2}\)
đang cần gấp ạ
Gía trị lớn nhất của :
B = -( x-3)2 + 5/4