Đáp án A

Vì ABC.A’B’C’ là lăng trụ đứng, đáy là tam giác vuông cân => C'(0;2;2)

Giống bài trước \(\Rightarrow B'\left(0;2;3\right)\Rightarrow M\left(\dfrac{1}{2};1;\dfrac{3}{2}\right)\)

\(\overrightarrow{AA'}=\left(0;0;3\right)=\overrightarrow{BB'}=\overrightarrow{CC'}\)

\(\Rightarrow\left\{{}\begin{matrix}B'\left(0;2;3\right)\\C'\left(-1;0;3\right)\end{matrix}\right.\)

\(\Rightarrow G\left(0;\dfrac{2}{3};3\right)\)

Gọi I là trung điểm của BC. Ta chứng minh được 

Suy ra I là hình chiếu của A 1  trên BC nên I(0;0;1)

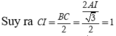
Chọn VTCP của 

Chọn D.

Đáp án D.

Đáp án D

Đáp án D.

Ta tìm được A ' x 0 ; 0 ; y 0 , C ' 0 ; 1 ; y 0 .

Gọi (P) là mặt phẳng chứa AC' và song song với B'C thì P : y 0 x + x 0 z − x 0 y 0 = 0 .

Do đó

d A C ' , B ' C = d C , P = x 0 y 0 x 0 2 + y 0 2 ≤ 2 2 . x 0 y 0 ≤ 2 4 x 0 + y 0 = 2

Dấu bằng xảy ra khi x 0 = y 0 = 2 .

Tam giác ABC có A B = 4 ; A C = B C = 5  nên có bán kính đường tròn ngoại tiếp là r = 5 2 . Ta lại có B B ' = 2  nên mặt cầu ngoại tiếp hình lăng trụ A B C . A ' B ' C '  có bán kính R = r 2 + 1 4 B B ' 2 = 29 2 .

Đáp án D.

Gọi O là trung điểm của AB, suy ra  O 0 ; 0 ; 0   .

Ta có A B → = − 2 x 0 ; 0 ; 0 , O C → = 0 ; 1 ; 0 ⇒ A B → . O C → = 0 ⇒ A B ⊥ O C .

Gắn hệ trục tọa độ Oxyz như hình vẽ bên. Với A x 0 ; 0 ; 0 , B − x 0 ; 0 ; 0 , C 0 ; 1 ; 0 , B ' − x 0 ; 0 ; 4 − x 0 , A ' x 0 ; 0 ; 4 − x 0 , C ' 0 ; 1 ; 4 − x 0  do   x 0 + y 0 = 4 và 0 < x 0 , y 0 < 4 .

 Có  A C ' → = − x 0 ; 1 ; 4 − x 0 , B ' C → = x 0 ; 1 ; x 0 − 4 ⇒ A C ' → , B ' C → = 2 x 0 − 8 ; 0 ; − 2 x 0

A C → = − x 0 ; 1 ; 0 ⇒ A C ' → , B ' C → . A C → = − x 0 2 x 0 − 8 = − 2 x 0 x 0 − 4

⇒ d A C ' ; B ' C = A C ' → , B ' C → . A C → A C ' → , B ' C → = 2 x 0 x 0 − 4 4 4 − x 0 2 + 4 x 0 2 = x 0 4 − x 0 4 − x 0 2 + x 0 2

 do x 0 ∈ 0 ; 4 .

Với  0 < x 0 < 4   , ta có 4 − x 0 2 + x 0 2 ≥ A M − G M 2 4 − x 0 2 x 0 2 = 2 x 0 4 − x 0 .

Như vậy d A C ' ; B ' C = x 0 4 − x 0 4 − x 0 2 + x 0 2 ≤ x 0 4 − x 0 2 x 0 4 − x 0 = 1 2 .

Dấu “=” xảy ra khi  x 0 = 4 − x 0 ⇔ x 0 = 2 = y 0   .

Khi đó A 2 ; 0 ; 0 , B − 2 ; 0 ; 0 , C 0 ; 1 ; 0 , B ' − 2 ; 0 ; 2 . Giả sử phương trình mặt cầu ngoại tiếp lăng trụ A B C . A ' B ' C '  là .

Ta có hệ phương trình sau:

  2 2 + 0 2 + 0 2 − 2 a .2 − 2 b .0 − 2 c .0 + d = 0 − 2 2 + 0 2 + 0 2 − 2 a − 2 − 2 b .0 − 2 c .0 + d = 0 0 2 + 1 2 + 0 2 − 2 a .0 − 2 b .1 − 2 c .0 + d = 0 − 2 2 + 0 2 + 2 2 − 2 a − 2 − 2 b .0 − 2 c .2 + d = 0 ⇔ 4 a − d = 4 4 a + d = − 4 2 b − d = 1 4 a − 4 c + d = − 8 ⇔ a = 0 b = − 3 2 c = 1 d = − 4

Vậy mặt cầu (S) có tâm I 0 ; − 3 2 ; 1  và bán kính 

R = a 2 + b 2 + c 2 − d = 29 2

Chọn D

Gọi I là trung điểm của BC => I(0; 0; 1)

=> I là hình chiếu vuông góc của  A 1 trên Oz

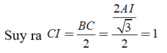
 (do tam giác ABC đều)

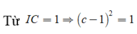
Trường hợp 1:  c= 0 (loại)

Trường hợp 2: c =2

Chọn VTCP của  A 1 C là