Trong không gian O x y z , cho hai điểm A 1 ; − 3 ; 2 , B 3 ; 5 ; − 2 . Phương trình mặt phẳng trung trực của đoạn AB có dạng x + a y + b z + c = 0. Khi đó a + b + c bằng
A. -3
B. 2
C. 4
D. -2
Trong không gian Oxyz, cho điểm A(1;-1;1) và hai đường thẳng ∆ : x - 1 2 = y 1 = z - 3 - 1 , ∆ ' : x 1 = y + 1 - 2 = z - 2 1 . Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng ∆ , ∆ ' là:
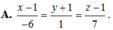
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng ∆ : x - 1 2 = y 1 = z - 3 - 1 , ∆ ' : x 1 = y + 1 - 2 = z - 2 1 .
Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng Δ, Δ' là:
![]()
![]()
![]()
![]()
Chọn C
Gọi d là đường thẳng cần tìm.

Đường thẳng cần tìm qua A và nhận ![]() là véc tơ chỉ phương nên có phương trình:
là véc tơ chỉ phương nên có phương trình:
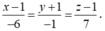
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d 1 : x - 1 2 = y - 1 - 1 = z + 1 1 , d 2 : x + 2 3 = y + 1 1 = z - 2 2 Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:
A. √38
B. 2√10
C. 8
D. 12
Chọn A
Vì A thuộc ![]() nên A (1+2t;1-t;-1+t).
nên A (1+2t;1-t;-1+t).
Vì B thuộc ![]() nên B (-2+3t';-1+t';2+2t').
nên B (-2+3t';-1+t';2+2t').

Thay vào (3) ta được t=1, t'=2 thỏa mãn.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3) và hai đường thẳng d 1 : x - 1 2 = y - 1 = z + 3 1 ; d 2 : x = 1 - t ; y = 2 t ; z = 1 . Viết phương trình đường thẳng △ đi qua A, vuông góc với cả d 1 và d 2
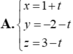
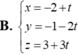
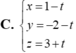

Trong không gian Oxyz cho hai đường thẳng d 1 : x + 1 3 = y - 1 2 = z - 2 - 1 , d 2 : x - 1 - 1 = y - 1 2 = z + 1 - 1 Đường thẳng ∆ đi qua điểm A(1;2;3) vuông góc với d 1 và cắt đường thẳng d 2 có phương trình là
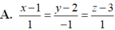
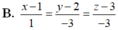
![]()
![]()
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;-2;3) và hai mặt phẳng (P):x+y+z+1=0;(Q):x-y+z-2=0. Phương trình nào dưới đây là phương trình đường thẳng qua A, song song với (P) và (Q).
A. x = 1 + 2 t y = - 2 z = 3 + 2 t
B. x = - 1 + t y = 2 z = - 3 - t
C. x = 1 y = - 2 z = 3 - 2 t
D. x = 1 + t y = - 2 z = 3 - t
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và hai đường thẳng d 1 : x − 2 2 = y + 2 − 1 = z − 3 1 và d 2 : x − 1 − 1 = y − 1 2 = z + 1 1 .Gọi ∆ là đường thẳng đi qua A, vuông góc với d 1 và cắt d 2 . Đường thẳng ∆ không nằm trong mặt phẳng nào dưới đây?
A. P 1 : x + 2 y − z − 2 = 0
B. P 2 : 2 x - y + z - 3 = 0
C. P 3 : x - 2 y + 2 z − 1 = 0
D. P 4 : x + 4 y + z − 12 = 0
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 2 2 = y + 2 - 1 = z - 3 1 và d 2 : x - 1 - 1 = y - 1 2 = z + 1 1 . Phương trình đường thẳng ∆ đi qua điểm A(1;2;3) vuông góc với d1 và cắt d2 là:
A. x - 1 1 = y - 2 - 3 = z - 3 - 5
B. x - 1 1 = y + 2 - 3 = z + 3 - 5
C. x + 1 - 1 = y + 2 3 = z + 3 5
D. x - 1 1 = y + 3 - 2 = z + 5 - 3
Trong không gian Oxyz, cho hai điểm A (1;0;0), B (0;0;2) và mặt cầu (S): x²+y²+z²-2x-2y+1=0. Hỏi có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với (S).
A.3.
B. 0
C. 1
D. 2
Chọn C
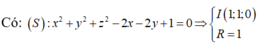
Gọi (P) là mặt phẳng thỏa mãn bài toán.
Ta có A (1; 0; 0) ∈ (S) => nếu tồn tại (P) thì (P) tiếp xúc với (S) tại A.
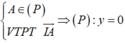
Ta thấy A (0; 0 ; 2) ∈ (P) duy nhất một mặt phẳng thỏa mãn bài toán.
Ghi chú: Bài toán này thường thường thì sẽ có hai mặt phẳng thỏa mãn, nhưng với số liệu của bài này thì chỉ có một mặt phẳng thỏa mãn bài toán.
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;-2;3) và hai mặt phẳng (P):x+y+z+1=0, (Q):x-y+z-2=0. Phương trình nào dưới đây là phương trình đường thẳng đi qua A, song song với (P) và (Q)?
A. x = - 1 + t y = 2 z = - 3 - t
B. x = 1 y = - 2 z = 3 - 2 t
C. x = 1 + 2 t y = - 2 z = 3 + 2 t
D. x = 1 + t y = - 2 z = 3 - t
Đáp Án D
Pt đường thẳng d có vecto chỉ phương u ⇀ = n P ⇀ , n Q ⇀ = (1;0;-1)
Dt đi qua A (1;-2;3)
Chọn đáp án D