Xét khai triển:

\(\left(1+x\right)^n=C_n^0+C_n^1x+C_n^2x^2+...+C_n^nx^n\)

\(\Leftrightarrow x\left(1+x\right)^n=C_n^0x+C_n^1x^2+C_n^2x^3+...+C_n^nx^{n+1}\)

Đạo hàm 2 vế:

\(\left(1+x\right)^n+nx\left(1+x\right)^{n-1}=C_n^0+2C_n^1x+3C_n^2x^2+...+\left(n+1\right)C_n^nx^n\)

Thay \(x=1\)

\(\Rightarrow2^n+n.2^{n-1}=1+2C_n^1+3C_n^2+...+\left(n+1\right)C_n^n\)

\(\Rightarrow2^{n-1}\left(2+n\right)-1=111\)

\(\Rightarrow2^{n-1}\left(2+n\right)=112=2^4.7\)

\(\Rightarrow n=5\)

\(\left(x^2+\dfrac{2}{x}\right)^5=\sum\limits^5_{k=0}C_5^kx^{2k}.2^{5-k}.x^{k-5}=\sum\limits^5_{k=0}C_5^k.2^{5-k}.x^{3k-5}\)

\(3k-5=4\Rightarrow k=3\Rightarrow\) hệ số: \(C_5^3.2^2\)

Bài 2:

a) Để B là phân số thì n -3 \(\ne\)0 => n\(\ne\)3

b) Để B có giá trị là số nguyên thì n+4 \(⋮\)n-3

\(\frac{n+4}{n-3}\)= \(\frac{n-3+7}{n-3}\)= \(\frac{7}{n-3}\)Vì n+4 \(⋮\)n-3 nên 7 \(⋮\)n-3

=> n-3 \(\in\)Ư(7) ={ 1;7; -1; -7}

=> n\(\in\){ 4; 10; 2; -4}

Vậy...

c) Bn thay vào r tính ra

la 120

Bài 1 :

Số hạng thứ 20 của biểu thức A là : 1+(20-1).6=115

Ta có biểu thức : 

A=1-7+13-19+25-31+...+109-115

=(1-7)+(13-19)+(25-31)+...+(109-115)  (có tất cả 10 cặp)

=(-6)+(-6)+(-6)+...+(-6)

=(-6).10=-60

Vậy giá trị của biểu thức A là -60.

Chúc bạn học tốt!

#Huyền#

Chọn A.

Áp dụng hệ thức  f(m + n) = f( m) + f( n) + mn

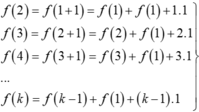
Vậy f( 2017) = 2017 + 2016.2017/2 = 20352153

f( 2016) = 2016 + 2015 + 2016/2 = 2033136

\(C_2^2+C_3^2+...+C_n^2=C_3^3+C_3^2+C_4^2+...+C_n^2\) (do \(C_2^2=C_3^3=1\))

\(=C_4^3+C_4^2+C_5^2+...+C_n^2=C_5^3+C_5^2+...+C_n^2\)

\(=...=C_n^3+C_n^2=C_{n+1}^3\)

Do đó:

\(2C_{n+1}^3=3A_{n+1}^2\Leftrightarrow\dfrac{2.\left(n+1\right)!}{3!.\left(n-2\right)!}=\dfrac{3.\left(n+1\right)!}{\left(n-1\right)!}\)

\(\Leftrightarrow n-1=9\Rightarrow n=10\)

\(\Rightarrow P=\left(1-x-3x^3\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(-x-3x^3\right)^k\)

\(=\sum\limits^{10}_{k=0}C_{10}^k\left(-1\right)^k\left(x+3x^3\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^kx^i.3^{k-i}.x^{3\left(k-i\right)}\)

\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^k.3^{k-i}.x^{3k-2i}\)

Ta có: \(\left\{{}\begin{matrix}0\le i\le k\le10\\i;k\in N\\3k-2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;2\right);\left(4;4\right)\)

Hệ số: \(C_{10}^2C_2^1\left(-1\right)^2.3^1+C_{10}^4C_4^4.\left(-1\right)^4.3^0=...\)

\(\Rightarrow he-so:\left[{}\begin{matrix}C^9_{10}C^1_9\left(-3\right)^{10-9}\left(-1\right)=270\\C^{10}_{10}C^4_{10}\left(-3\right)^{10-10}.\left(-1\right)^4=210\end{matrix}\right.\)

Đáp án A.

A

Chọn A