Hàm số nào sau đây luôn đồng biến trên tập xác định của nó
A. y = x − 1 2 − x
B. y = 1 − 2 x 1 − x
C. y = x + 1 2 x + 1
D. y = 2 x x − 1
Những câu hỏi liên quan
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:54
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. \(y = {\log _{0,5}}x\).
B. \(y = {{\rm{e}}^{ - x}}\).
C. \(y = {\left( {\frac{1}{3}} \right)^x}\).
D. \(y = \ln x\).
Chọn D. Bởi vì hàm số ln x luôn luôn dương nên chắc chắn sẽ đồng biến trên TXĐ của nó
Đúng 0
Bình luận (0)
SGK Cánh Diều
13 tháng 8 2023 lúc 21:34
Đề bài
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. \(y = {(0,5)^x}\)
B. \(y = {\left( {\frac{2}{3}} \right)^x}\)
C. \(y = {(\sqrt 2 )^x}\)
D. \(y = {\left( {\frac{e}{\pi }} \right)^x}\)
Vì \(\sqrt{2}\simeq1,414>1\)
⇒ Hàm số \(y=\left(\sqrt{2}\right)^x\) đồng biến trên R.
⇒ Chọn C.
Đúng 1
Bình luận (0)
căn 2>1
=>y=(căn 2)^x đồng biến
=>Chọn C
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:53
Cho hàm số y=2x. Khẳng định nào sau đây là sai?
A. Tập xác định của hàm số là R.
B. Tập giá trị của hàm số là (0;+∞).
C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.
D. Hàm số đồng biến trên tập xác định của nó.
Đồ thị này cắt trục Ox tại rất nhiều điểm chứ không phải chỉ có 1 điểm
=>Chọn C
Đúng 0
Bình luận (0)
Trong các hàm số sau đây, hàm số nào đồng biến trên tập xác định của nó? A.
y
log
a
x
với
a
1
5
6
-
5
B.
y
log
2
3
x...
Đọc tiếp
Trong các hàm số sau đây, hàm số nào đồng biến trên tập xác định của nó?
A. y = log a x với a = 1 5 6 - 5
B. y = log 2 3 x
C. y = log π 4 x
D. y = log 2 x
Trong các hàm số sau đây, hàm số nào đồng biến trên tập xác định của nó
Hàm số nào sau đây đồng biến trên tập xác định của nó? A.
y
3
π
x
B.
y
2
+
3
e
x...
Đọc tiếp
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. y = 3 π x
B. y = 2 + 3 e x
C. y = 2020 - 2019 x
D. y = log 1 2 x + 4
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
y
2
x
+
1
x
+
1
(I) ; y -x4 + x2 – 2 (II); y x3 – 3x – 5 (III). A. I và II B. Chỉ I C. I và III D. II và III
Đọc tiếp
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
y = 2 x + 1 x + 1 (I) ; y = -x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
A. I và II
B. Chỉ I
C. I và III
D. II và III
Chọn B.
Hàm số (I): 
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=>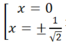 
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.
Đúng 0
Bình luận (0)
Trong các hàm số sau,hàm số nào luôn nghịch biến trên tập xác định của nó?
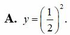
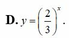
Cho hàm số y=\(\sqrt{2-x+2\sqrt{1}-x}\)
1,tìm tập xác định của hàm số
2,xét hàm số đồng biến,nghịch biến trên tập xác định của nó