Gọi z 1 , z 2 , z 3 , z 4 là nghiệm của phương trình ( z - 1 2 z - i ) 4 =1. Giá trị của ( z 1 . z 2 . z 3 . z 4 ) 2 bằng
A. 2i
B. i
C. 0
D. -1
Những câu hỏi liên quan
Cho các số phức
z
1
1
,
z
2
2
−
3
i
và các số z thỏa mãn
z
−
1
−
i
+
z
−
3
+
i
2
2
....
Đọc tiếp
Cho các số phức z 1 = 1 , z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i + z − 3 + i = 2 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z − z i + z − z 2 . Tính tổng
A. S = 4 + 2 5 .
B. S = 5 + 17 .
C. S = 1 + 10 + 17 .
D. S = 10 + 2 5 .
Cho các số phức
z
1
1,
z
2
2
−
3
i
và các số z thỏa mãn
z
−
1
−
i
+
z
−
3
+
i
2
2
.
Gọi M, m...
Đọc tiếp
Cho các số phức z 1 = 1, z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i + z − 3 + i = 2 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z − z i + z − z 2 . Tính tổng S = M + m
A. S = 4 + 2 5 .
B. S = 5 + 17 .
C. S = 1 + 10 + 17 .
D. S = 10 + 2 5 .
Đáp án B.
Số phức z 1 = 1 có điểm biểu diễn là A 1 ; 0 , số phức z 2 = 2 − 3 i có điểm biểu diễn là B 2 ; − 3
Gọi E x ; y là điểm biểu diễn của số phức z, khi đó z = x + y i , x , y ∈ ℝ
Suy ra
P = x − 1 + y i + x − 2 + y + 3 i = x − 1 2 + y 2 + x − 2 2 + y + 3 2
⇒ P = E A + E B .
Mặt khác
z − 1 − i + z − 3 + i = 2 2 ⇔ x − 1 + y − 1 i + x − 3 + y + 1 i = 2 2
⇔ x − 1 2 + y − 1 2 + x − 3 2 + y + 1 2 = 2 2 *
Gọi M 1 ; 1 , N 3 ; − 1 thì E M + E N = 2 2 = M N ⇒ Điểm E thuộc đoạn MN.
Ta có phương trình đường thẳng MN là x + y + z − 2 = 0 với x ∈ 1 ; 3
Bài toán trở thành:
Cho điểm E thuộc đoạn MN . Tìm giá trị lớn nhất của biểu thức P = E A + E B
Đặt f ( x ) = x + y − 2. Ta có
f 1 ; 0 = 1 + 0 − 2 = − 1 f 2 ; − 3 = 2 − 3 − 2 = − 3 ⇒ f 1 ; 0 . f 2 ; − 3 = 3 > 0 . Suy ra hai điểm A,B nằm cùng về một phía đối với MN . Gọi A' là điểm đối xứng với A qua MN thì A ' 2 ; 1 .Khi đó
P = E A + E B = E A ' + E B ≥ A ' B = 4 .
Dấu = xảy ra khi và chỉ khi
E ∈ A ' B ⇒ E = A ' B ∩ M N ⇒ E 2 ; 0 hay z = 2.
Do điểm E luôn thuộc đường thẳng MN nên P = E A + E B đạt giá trị lớn nhất khi E ≡ M hoặc E ≡ N .
Có
M A + M B = 1 + 17 N A + N B = 2 5 ⇒ M A + M B > N A + N B ⇒ max P = M A + M B = 1 + 17.
Vậy
M = 1 + 7 , m = 4 ⇒ S = M + m = 5 + 17 .
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn |z - 3 - 4i|
5
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P
|
z
+
2
|
2
-
|
z
-
1
|
2
. Tính mô đun của số phức
ω
M + mi A. |
ω
|
1258
B. |...
Đọc tiếp
Cho số phức z thỏa mãn |z - 3 - 4i| = 5 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = | z + 2 | 2 - | z - 1 | 2 . Tính mô đun của số phức ω = M + mi
A. | ω | = 1258
B. | ω | = 3 137
C. | ω | = 2 134
D. | ω | = 2 309
Đáp án A
Đặt z = x + yi
Có 
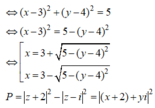
TH1:
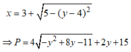
Xét hàm số: 
trên 
Có
Ta có:
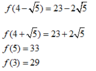
TH2:
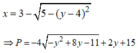
Xét hàm số: 
trên 
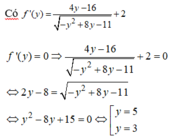
Ta có:
Đúng 0
Bình luận (0)
Gọi S là tập hợp các số phức z có phần thực và phần ảo đều là các số nguyên đồng thời thoả mãn hai điều kiện:
z
-
3
-
4
i
≤
2
và
z
+
z
¯
≤
z
-
z
¯...
Đọc tiếp
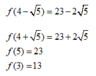
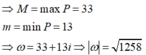
Gọi S là tập hợp các số phức z có phần thực và phần ảo đều là các số nguyên đồng thời thoả mãn hai điều kiện: z - 3 - 4 i ≤ 2 và z + z ¯ ≤ z - z ¯ . Số phần tử của tập S bằng
A. 11.
B. 12.
C. 13.
D. 10.
Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| | 2
z
¯
- z + 3i | . Tập hợp tất cả những điểm M như vậy là A. một parabol. B. một đường thẳng. C. một đường tròn. D. một elip.
Đọc tiếp
Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| = | 2 z ¯ - z + 3i | . Tập hợp tất cả những điểm M như vậy là
A. một parabol.
B. một đường thẳng.
C. một đường tròn.
D. một elip.
Chọn A.
Gọi số phức z = x + yi có điểm biểu diễn là M(x; y) trên mặt phẳng tọa độ:
Theo đề bài ta có:
⇔ |3(x + yi) + 3i| = |2(x – yi) – (x + yi) + 3i
⇔ |3x + (3y + 3)i| = |x + (3 – 3y)|
Hay 9x2 + ( 3y + 3) 2 = x2 + ( 3 - 3y) 2
Suy ra: 8x2 + 36y = 0 hay y = -2/9 x2
Vậy tập hợp các điểm M(x; y) biểu diễn số phức z theo yêu cầu của đề bài là parabol 
Đúng 0
Bình luận (0)
Số phức z thỏa mãn z^6-z^5+z^4-z^3+z^2-z+1=0. Tìm phần thực của w=z(z^2-z+1).
Cho số phức z thỏa mãn
z
−
1
+
i
+
z
+
2
−
3
i
5
và
w
z
−
i
. Gọi T là giá trị lớn nhất của
w
. Tìm T. A.
T
5...
Đọc tiếp
Cho số phức z thỏa mãn z − 1 + i + z + 2 − 3 i = 5 và w = z − i . Gọi T là giá trị lớn nhất của w . Tìm T.
A. T = 5
B. T = 2 5
C. T = 2 2
D. T = 2 5
Cho số phức z thỏa mãn
z
−
1
+
i
+
z
+
2
−
3
i
5
và
w
z
−
i
. Gọi T là giá trị lớn nhất của |w|. Tìm T. A.
T
5
B.
T...
Đọc tiếp
Cho số phức z thỏa mãn z − 1 + i + z + 2 − 3 i = 5 và w = z − i . Gọi T là giá trị lớn nhất của |w|. Tìm T.
A. T = 5
B. T = 2 5
C. T = 2 2
D. T = 2 5
Cho số phức z thỏa mãn \(z^6-z^5+z^4-z^3+z^2-z+1=0\)Tìm phần thực của \(w=z\left(z^2-z+1\right)\)
Tìm x, y, z
dfrac{x+y+2}{z}dfrac{y+z+1}{x}dfrac{z+x-3}{y}dfrac{1}{x+y+z}
Áp dụng tích chất của dãy tỉ số bằng nhau, ta có
dfrac{x+y+2}{z}dfrac{y+z+1}{x}dfrac{z+x-3}{y}
dfrac{x+y+2+y+z+1+z+x-3}{z+x+y}dfrac{2left(x+y+zright)+left(1+2-3right)}{z+x+y}2
Vìdfrac{x+y+2}{z}dfrac{y+z+1}{x}dfrac{z+x-3}{y}dfrac{1}{x+y+z}
2dfrac{1}{x+y+z}2left(x+y+zright)1x+y+zdfrac{1}{2}
dfrac{x+y+2}{z}2x+y+22z
dfrac{y+z+1}{x}2y+z+12x
dfrac{z+x-3}{y}2z+x-32y
dfrac{1}{x+y+z}2x+y+zdfrac{1}{2}
+) x+y+z dfrac{1}{2}y+zdfra...
Đọc tiếp
Tìm x, y, z
\(\dfrac{x+y+2}{z}=\dfrac{y+z+1}{x}=\dfrac{z+x-3}{y}=\dfrac{1}{x+y+z}\)
Áp dụng tích chất của dãy tỉ số bằng nhau, ta có
\(\dfrac{x+y+2}{z}=\dfrac{y+z+1}{x}=\dfrac{z+x-3}{y}\\ =\dfrac{x+y+2+y+z+1+z+x-3}{z+x+y}=\dfrac{2\left(x+y+z\right)+\left(1+2-3\right)}{z+x+y}=2\\ Vì\dfrac{x+y+2}{z}=\dfrac{y+z+1}{x}=\dfrac{z+x-3}{y}=\dfrac{1}{x+y+z}\\ =>2=\dfrac{1}{x+y+z}=>2\left(x+y+z\right)=1=>x+y+z=\dfrac{1}{2}\\ =>\dfrac{x+y+2}{z}=2=>x+y+2=2z\\ \dfrac{y+z+1}{x}=2=>y+z+1=2x\\ \dfrac{z+x-3}{y}=2=>z+x-3=2y\\ \dfrac{1}{x+y+z}=2=>x+y+z=\dfrac{1}{2}\)
+) x+y+z = \(\dfrac{1}{2}=>y+z=\dfrac{1}{2}-x=>\dfrac{1}{2}-x+1=2x=>3x=\dfrac{3}{2}=>x=\dfrac{1}{2}\)
+)\(x+y+z=\dfrac{1}{2}=>x+y=\dfrac{1}{2}-z=>\dfrac{1}{2}-z+2=2z=>3z=\dfrac{5}{2}=>z=\dfrac{5}{6}\)
\(=>x+y+z=\dfrac{1}{2}+\dfrac{5}{6}+y=\dfrac{1}{2}=>\dfrac{4}{3}+y=\dfrac{1}{2}=>y=\dfrac{-5}{6}\)
Vậy \(x=\dfrac{1}{2}\\ y=\dfrac{-5}{6}\\ z=\dfrac{5}{6}\)
Ê mấy bọn 7B Nguyễn Lương Bằng ơi bài 2 Toán chiều làm thế này đúng chưa! Góp ý nha!
Xem thêm câu trả lời