Chọn A.

Ta có  và tam giác ABC nhọn nên A = 45º.

A + B + C = 180 º ⇒ B + C = 180º - 45º = 135º

Do 3 góc tam giác lập thành cấp số cộng ; số đo góc A nhỏ nhất nên B = A + d; C = A + 2d.

Khi đó: B + C = A + d + A + 2d = 2A + 3d ⇒ 3d = 135º - 2.45º = 45º

⇒ d = 15º ⇒ B = A + d = 60º; C = A + 2d = 75º

  Đã xảy ra lỗi rồi. Bạn thông cảm vì sai sót này.

  Ta có:  

Áp dụng hệ quả của bất đẳng thức Cauchy cho ba số không âm 

   trong đó với     , ta có:

Tương tự, ta có:

Cộng ba bất đẳng thức     và   , ta được:

Khi đó, ta chỉ cần chứng minh

Thật vậy, bất đẳng thức cần chứng minh được quy về dạng sau:    (bất đẳng thức Cauchy cho ba số   )

Hay       

Mà    đã được chứng minh ở câu    nên    luôn đúng với mọi  

Dấu    xảy ra    

Vậy,       

đặt AB=c, BC=a, AC=c.
để chứng minh bđt trên ta sẽ áp dụng công thức: \(S_{\Delta ABC}=\frac{1}{2}.a.b.sinC=\frac{1}{2}.b.c.sinA=\frac{1}{2}.a.c.sinB\)
ta có: \(\frac{sinA}{sinB+sinC}+\frac{sinB}{sinA+sinC}+\frac{sinC}{sinA+sinB}\)
       \(=\frac{a.b.c.sinA}{a.b.c.sinB+a.b.c.sinC}+\frac{a.b.c.sinB}{a.b.c.sinA+a.b.c.sinC}+\frac{a.b.c.sinC}{a.b.c.sinA+a.b.c.sinB}\)
        ;\(=\frac{2S_{\Delta ABC}.a}{2S_{\Delta ABC}.b+2S_{\Delta ABC}.c}+\frac{2S_{\Delta ABC}.b}{2.S_{\Delta ABC}.c+2.S_{\Delta ABC}.b}+\frac{2S_{\Delta ABC}.c}{2S_{\Delta ABC}.b+2S_{\Delta ABC}.a}\)
         \(=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\).
Ta có: \(\frac{a}{b+c}>\frac{a}{a+b+c};\frac{b}{a+c}>\frac{b}{a+b+c};\frac{c}{a+b}>\frac{c}{a+b+c}\)
nên \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=1.\)
Ta sẽ chứng minh bđt phụ: \(\frac{a}{b+c}< \frac{2a}{a+b+c}\left(1\right)\)
Thật vậy: \(\left(1\right)\Leftrightarrow a^2< a\left(b+c\right)\Leftrightarrow a< b+c\)(đúng vì a,b,c là độ dài 3 cạnh của tam giác).
tương tự: \(\frac{b}{a+c}< \frac{2b}{a+b+c};\frac{c}{a+b}< \frac{2c}{a+b+c}\).
suy ra: \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}< \frac{2a}{b+c}+\frac{2b}{a+c}+\frac{2c}{a+b}=\frac{2\left(a+b+c\right)}{a+b+c}=2\).
vậy bất đẳng thức đã được chứng minh.
 

câu này khó ghê

ô mai nhót . Bài toàn khó thế này mà giải được . Tài thật 

a) Theo định lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \to b = \frac{{a.\sin B}}{{\sin A}}\) thay vào \(S = \frac{1}{2}ab.\sin C\) ta có:

\(S = \frac{1}{2}ab.\sin C = \frac{1}{2}a.\frac{{a.\sin B}}{{\sin A}}.sin C = \frac{{{a^2}\sin B\sin C}}{{2\sin A}}\) (đpcm)

b) Ta có: \(\hat A + \hat B + \hat C = {180^0} \Rightarrow \hat A = {180^0} - {75^0} - {45^0} = {60^0}\)

\(S = \frac{{{a^2}\sin B\sin C}}{{2\sin A}} = \frac{{{{12}^2}.\sin {{75}^0}.\sin {{45}^0}}}{{2.\sin {{60}^0}}} = \frac{{144.\frac{1}{2}.\left( {\cos {{30}^0} - \cos {{120}^0}} \right)}}{{2.\frac{{\sqrt 3 }}{2}\;}} = \frac{{72.(\frac{{\sqrt 3 }}{2}-\frac{{-1 }}{2}})}{{\sqrt 3 }} = 36+12\sqrt 3 \)

a: Xét ΔABC có \(AB^2=AC^2+BC^2\)

nên ΔABC vuông tại C

Ta có:

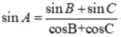
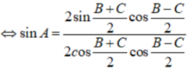
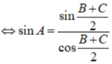
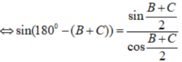
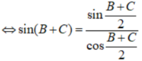
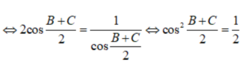
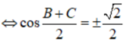
Vì:

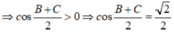
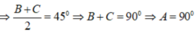
Suy ra, tam giác ABC vuông tại A