Cho một cấp số cộng u n có u 1 = 0 và tổng 100 số hạng đầu bằng 24850. Tính S = 1 u 1 u 2 + 1 u 2 u 3 + . . . + 1 u 49 u 50 .
A. S = 123 .
B. S = 4 23 .
C. S = 9 246 .
D. S = 49 246 .
Cho một cấp số cộng u n có u 1 = 1 và tổng 100 số hạng đầu bằng 24850. Tính S = 1 u 1 u 2 + 1 u 2 u 3 + . . . + 1 u 49 u 50
A. S=123
B. 4 23
C. 9 246
D. 49 246
Cho một cấp số cộng u n có u 1 = 1 và tổng 100 số hạng đầu bằng 24850. Tính S = 1 u 1 u 2 + 1 u 2 u 3 + ... + 1 u 49 u 50
A. S = 123
B. S = 4 23
C. S = 9 246
D. S = 49 246
Đáp án D
Ta có
u 1 = 1 S 100 = 24850 ⇔ u 1 = 1 100 2 u 1 + 99 d = 24850 ⇒ u 1 = 1 d = 5 ⇒ u n − u n − 1 5 = 1
Khi đó
5 S = 5 u 1 u 2 + 5 u 2 u 3 + ... + 5 u 49 u 50 = u 2 − u 1 u 1 u 2 + u 3 − u 2 u 2 u 3 + ... + u 50 − u 49 u 49 u 50 = 1 u 1 − 1 u 2 + 1 u 2 − 1 u 3 + ... + 1 u 49 − 1 u 50 = 1 − 1 u 50 = 1 − 1 u 1 + 49 d = 245 246 ⇒ S = 49 246
Cho một cấp số cộng (un) có u1 = 1 và tổng 100 số hạng đầu bằng 24850. Tính S = 1 u 1 u 2 + 1 u 2 u 3 + . . . . . . 1 u 49 u 50
A. S = 9 246
B. S = 4 23
C. S = 123
D. S = 49 246
Chọn D.
Gọi d là công sai của cấp số đã cho
Ta có: S100 = 50(2u1 +99d) = 24850 ⇒ ![]()
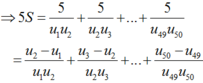
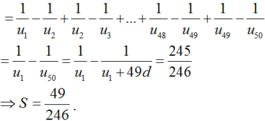
Cho một cấp số cộng u n có u 1 = 1 và tổng của 100 số hạng đầu bằng 24850. Biểu thức S = 1 u 1 u 2 + 1 u 2 u 3 + . . . + 1 u 49 u 50 bằng
A. 49 246
B. 9 246
C. 123
D. 4 23
Cho một cấp số cộng (un) có u1 = 1 và tổng của 100 số hạng đầu bằng 24850. Biểu thức S = 1 u 1 u 2 + 1 u 2 u 3 + . . + 1 u 49 u 50 bằng
A. S = 9 246
B. S = 49 246
C. S = 123
D. S = 4 23
Đáp án A
Gọi d là công sai của cấp số đã cho.
Ta có:
![]()
⇒ d = 497 - 2 u 1 99 = 5
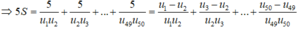
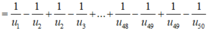
![]()
⇒ S = 49 246
Cho cấp số cộng u n có u 1 = 1 và tổng 100 số hạng đầu là 24850. Tính tổng S = 1 u 1 u 2 + 1 u 2 u 3 + ... + 1 u 49 u 50
A. S = 124.
B. S = 4 23 .
C. S = 49 246 .
D. S = 17 246 .
Cho một cấp số cộng ( u n ) , u 1 = 1 và tổng 100 số hạng đầu tiên là 24850. Tính S = 1 u 1 u 2 + 1 u 2 u 3 + . . . + 1 u 49 u 50
A. S = 9 242
B. S = 4 23
C. S = 33 125
D. S = 49 246
Cho cấp số cộng u n có u n và tổng 100 số hạng đầu là 24850. Tính tổng S = 1 u 1 u 2 + 1 u 2 u 3 + ... + 1 u 49 u 50
A. S = 124.
B. S = 4 23 .
C. S = 49 246 .
D. S = 17 246 .
Đáp án C
Ta có S 100 = 50 2 u 1 + 99 d ⇒ d = 5
⇒ 5 S = 5 u 1 u 2 + 5 u 2 u 3 + ... + 5 u 49 u 50 = u 2 − u 1 u 1 u 2 + u 3 − u 3 u 2 u 3 + ... + u 50 − u 49 u 49 u 50
= 1 u 1 − 1 u 2 + 1 u 2 − 1 u 3 + ... + 1 u 49 − 1 u 50 = 1 u 1 − 1 u 1 + 49 d = 245 246 ⇒ S = 49 246
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77