Tìm tập hợp tất cả các nghiệm thực của bất phương trình 9 7 3 x − 2 x 2 ≥ 9 7 .
A. x ∈ 1 2 ; 1
B. x ∈ 1 2 ; 1
C. x ∈ − ∞ ; 1 2 ∪ 1 ; + ∞
D. x ∈ − ∞ ; 1 2 ∪ 1 ; + ∞
Gọi S là tập hợp tất cả giá trị nguyên dương và nhỏ hơn 9 của m để bất phương trình x2 + 6x <= 2m( |x + 3| - 2 ) - 6 có nghiệm thực. Tính tổng tất cả các phần tử của S
S là tập hợp tất cả các giá trị thực của tham số a thỏa mãn mỗi nghiệm của bất phương trình log x ( 5 x 2 - 8 x + 3 ) > 2 đều là nghiệm của bất phương trình x 2 - 2 x - a 4 + 1 ≥ 0 . Khi đó:
A. S = - 10 5 ; 10 5 .
B. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞
C. S = - 10 5 ; 10 5 .
D. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞ .
Xét bất phương trình 3 3 x - 4 . 3 x + 1 + 3 m - 5 < 0 . Tập hợp tất cả các giá trị thực của tham số m để bất phương trình đã cho có nghiệm thực là
A. ( - ∞ ; 7 ]
B. - ∞ ; 5 3
C. - ∞ ; 3
D. - ∞ ; 7
Chọn đáp án D.

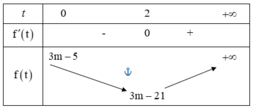
Từ bảng biến thiên trên, ta có bất phương trình đã cho có nghiệm khi và chỉ khi bất phương trình f(t) < 0
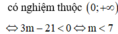
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình 3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11.
B. m ≥ -11.
C. m < -11.
D. m ≤ -11.
Chọn A.
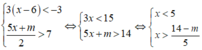
Hệ bất phương trình có nghiệm
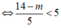 ⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
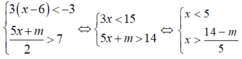
Hệ bất phương trình có nghiệm 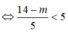
hay 14 - m < 25 hay m > -11
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
3 ( x - 6 ) < - 3 5 x + m 2 > 7 có nghiệm.
A. m > -11
B. m ≥ -11
C. m < -11
D. m ≤ -11
Chọn A
Ta có:
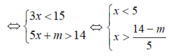
Hệ bất phương trình có nghiệm ⇔ 14 - m 5 < 5
Hay 14 - m < 25 tương đương m > -11
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. - ∞ ; 3
B. - ∞ ; 3
C. ( 3 2 ; + ∞ )
D. ( - ∞ ; 3 2 )
Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 − x ≥ m
A. − ∞ ; 3
B. − ∞ ; 3 2
C. 3 2 ; + ∞
D. − ∞ ; 3 2
Đáp án B
Điều kiện x + 5 ≥ 0 4 − x ≥ 0 ⇔ − 5 ≤ x ≤ 4
Xét hàm số f x = x + 5 + 4 − x ; x ∈ − 5 ; 4
Ta có:
f ' x = 1 2 x + 5 − 1 2 4 − x ; f ' x = 0 ⇔ 4 − x = x + 5 ⇔ x = − 1 2
Tính các giá trị f − 5 = 3 ; f 4 = 3 ; f − 1 2 = 3 2
⇒ max − 5 ; 4 f x = f − 1 2 = 3 2
Vậy để phương trình m ≤ f x có nghiệm m ≤ max − 5 ; 4 f x ⇔ m ≤ 3 2