Cho a, b là các số dương thỏa mãn log 9 a = log 16 b = log 12 5 b - a 2 . Tính giá trị a b
A. a b = 3 + 6 4
B. a b = 7 - 2 6
C. a b = 7 + 2 6
D. a b = 3 - 6 4
Những câu hỏi liên quan
Cho các số thực dương a,b thỏa mãn
log
a
x
,
log
b
y
. Tính
P
log
(
a
2
b
3
)
Đọc tiếp
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
Cho a,b là các số thực thỏa mãn log 2 . log 2 a - log b = 2 . Hỏi a,b thỏa mãn hệ thức nào dưới đây?
A. a = 100b
B. a = 100 - b
C. a = =100 + b
D. a = 100 b
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
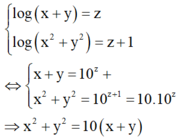
Khi đó
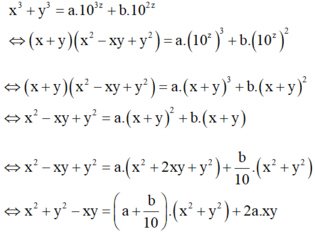
Đồng nhất hệ số, ta được
Đúng 0
Bình luận (0)
Giả sử a,b là các số thực sao cho
x
3
+
y
3
a
10
3
x
+
b
10
2
x
đúng với mọi các số thực dương x, y, z thỏa mãn
log
(
x
+
y...
Đọc tiếp
Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
SGK Cánh Diều
13 tháng 8 2023 lúc 21:10
Đề bài
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 100\). Tính giá trị của biểu thức \(P = 3\log a + 2\log b\)
\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)
Đúng 0
Bình luận (0)
Cho các số thực dương a,b thỏa mãn
log
a
x
,
log
b
y
. Tính
l
o
g
(
a
2
b
3
)
? A. 6xy B.
x
3
y
3
C.
x
3
+
y
3
D. 2x+3y
Đọc tiếp
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính l o g ( a 2 b 3 ) ?
A. 6xy
B. x 3 y 3
C. x 3 + y 3
D. 2x+3y
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:15
Đặt \(\log 2 = a,\log 3 = b\). Biểu thị các biểu thức sau theo \(a\) và \(b\).
a) \({\log _4}9\);
b) \({\log _6}12\);
c) \({\log _5}6\).
a: \(log_49=\dfrac{log9}{log4}=\dfrac{log3^2}{log2^2}=\dfrac{2\cdot log3}{2\cdot log2}=\dfrac{log3}{log2}=\dfrac{b}{a}\)
b: \(log_612=\dfrac{log12}{log6}=\dfrac{log2^2+log3}{log2+log3}=\dfrac{2\cdot log2+log3}{log2+log3}\)
\(=\dfrac{2a+b}{a+b}\)
c: \(log_56=\dfrac{log6}{log5}=\dfrac{log\left(2\cdot3\right)}{log\left(\dfrac{10}{2}\right)}=\dfrac{log2+log3}{log10-log2}\)
\(=\dfrac{a+b}{1-a}\)
Đúng 1
Bình luận (0)
a: l o g 4 9 = l o g 9 l o g 4 = l o g 3 2 l o g 2 2 = 2 ⋅ l o g 3 2 ⋅ l o g 2 = l o g 3 l o g 2 = b a log 4 9= log4 log9 = log2 2 log3 2 = 2⋅log2 2⋅log3 = log2 log3 = a b b: l o g 6 12 = l o g 12 l o g 6 = l o g 2 2 + l o g 3 l o g 2 + l o g 3 = 2 ⋅ l o g 2 + l o g 3 l o g 2 + l o g 3 log 6 12= log6 log12 = log2+log3 log2 2 +log3 = log2+log3 2⋅log2+log3 = 2 a + b a + b = a+b 2a+b c: l o g 5 6 = l o g 6 l o g 5 = l o g ( 2 ⋅ 3 ) l o g ( 10 2 ) = l o g 2 + l o g 3 l o g 10 − l o g 2 log 5 6= log5 log6 = log( 2 10 ) log(2⋅3) = log10−log2 log2+log3 = a + b 1 − a = 1−a a+b
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:13
Tính giá trị các biểu thức sau:
a) \({\log _2}16\);
b) \({\log _3}\frac{1}{{27}}\);
c) \(\log 1000\);
d) \({9^{{{\log }_3}12}}\).
a) \(log_216=4\)
b) \(log_3\dfrac{1}{27}=-3\)
c) \(log1000=3\)
d) \(9^{log_312}=144\)
Đúng 1
Bình luận (0)