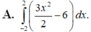
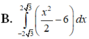
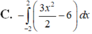
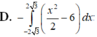
Diện tích hình phẳng giới hạn bởi hai parabol y = 1 2 x 2 và y = 6 - x 2 bằng
A. ∫ - 2 2 3 x 2 2 - 6 d x
B. ∫ - 2 3 2 3 x 2 2 - 6 d x
C. ∫ - 2 2 3 x 2 2 - 6 d x
D. ∫ - 2 3 2 3 x 2 2 - 6 d x
Tình diện tích hình phẳng giới hạn bởi parabol y = - x 2 và đường thẳng y = - x - 2
A. 2
B. 9 2
C. 1
D. 3 4
Diện tích của hình phẳng giới hạn bởi parabol y = 2 - x 2 và đường thẳng y = - x
A. 9 4
B. 9 2
C. 9
D. 18
Tình diện tích hình phẳng giới hạn bởi parabol y = –x2 và đường thẳng y = –x – 2.
A. 2
B. 9 2
C. 1
D. 3 4
Diện tích của hình phẳng giới hạn bởi parabol y = 2 - x 2 và đường thẳng y = - x là
A. S = 9 4
B. S = 9 2
C. S = 9
D. S = 18
Chọn B.
Phương pháp: Tìm hoành độ giao điểm và lấy tích phân để tích diện tích.
Cách giải: Phương trình hoành độ giao điểm là:
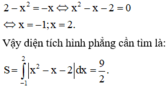
Tính diện tích S của hình phẳng giới hạn bởi đường parabol y = x 3 - 3 x + 2 và đường thẳng y=x-1.
A. S = 3 4
B. S = 2
C. S = 37 14
D. S = 799 300
Diện tích hình phẳng giới hạn bởi parabol y= ( x - 2 ) 2 , đường cong y= x 3 và trục hoành bằng (phần tô đậm trong hình vẽ bên)
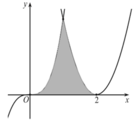
A. 11 2
B. 73 12
C. 7 12
D. 5 2
Chọn đáp án C.
Phương trình hoành độ giao điểm:
Tính diện tích hình phẳng giới hạn bởi parabol và đường thẳng y = x
A. 9 2
B. 11 6
C. 27 6
D. 17 6
Trong hệ trục tọa độ Oxyz, cho Parabol P : y = x 2 và hai đường thẳng y = a , y = b 0 < a < b (hình vẽ). Gọi S 1 là diện tích hình phẳng giới hạn bởi parabol (P) đường thẳng y = a và đường thẳng y = b (phần gạch chéo) và S 2 là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng y = a (phần tô đậm). Với điều kiện nào sau đây của a và b thì S 1 = S 2
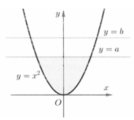
A. b = 4 a 3
B. b = 2 a 3
C. b = 3 a 3
D. b = 6 a 3
