Gọi S là tập nghiệm của bất phương trình 2 x 3 + x ≤ x + 2 2 x + 5 . Biết S = a ; b , a , b ∈ ℝ . Giá trị M = a 2 b 3 của gần nhất với số nào sau đây:
A. 0,12
B. 2,42
C. 2,12
D. 1,12
Gọi S là tập nghiệm của bất phương trình \(\dfrac{x^2+x+3}{x^2-4}\ge1\) . Khi đó S \(\cap\left(-2;2\right)\) là tập nghiệm nào
\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
gọi S là tập nghiệm của bất phương trình \(x^2-\left(2m-6\right)x+m^2-6m+5\le0\). tìm tất cả các giá trị của m sao cho (3;5) \(\subset\) S.
=>x^2-[(m-1)+(m-5)]x+m^2-6m+5<=0
=>x(x-m+1)-(m-5)(x-m+1)<=0
=>(x-m+1)(x-m+5)<=0
=>m-5<=x<=m-1
=>S=[m-5;m-1]
(3;5) là tập con của S
=>m-5>=3 và m-1<=5
=>m>=8 và m<=6
=>Loại
1.Bất phương trình (m2-3m)x+m<2-2x vô nghiệm khi:
a.m#1 b.m#2 c.m=2 d.=3
2.Gọi S là tập hợp tất cả các giá trị thực của tham số m để bất phương trình (m2-m)x +m<6x-2
GIUP MÌNH VỚI Ạ
Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)
Tập nghiệm của bất pt
a) \(\dfrac{x-2}{x+1}\ge\dfrac{x+1}{x-2}\)
b) Gọi S là nghiệm của bất pt \(\dfrac{x^2+x+3}{x^2-4}\ge1\). Khi đó \(S\cap\left(-2;2\right)\) là tập nào
a, \(\dfrac{x-2}{x+1}\ge\dfrac{x+1}{x-2}\)
⇔ \(\dfrac{\left(x-2\right)^2-\left(x+1\right)^2}{\left(x-1\right)\left(x+2\right)}\ge0\)
⇔ \(\dfrac{3-6x}{\left(x+1\right)\left(x-2\right)}\) ≥ 0
⇔ \(\dfrac{2x-1}{\left(x+1\right)\left(x-2\right)}\) ≤ 0
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\-1< x< 2\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\\left[{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}\le x< 2\\x< -1\end{matrix}\right.\)
Vậy tập nghiệm là \(\left(-\infty;-1\right)\cup\) \(\left[\dfrac{1}{2};2\right]\)\ {2}
Bạn có thể biến cái ngoặc vuông kia (ở chỗ số 2) thành ngoặc tròn
Còn vì sao mình không biến cái ngoặc vuông kia (ở chỗ số 2) thành ngoặc tròn thì đó là một câu chuyện dài
b, tương tự, chuyển vế đổi dấu
\(\left(3-m\right)x>-m^2+4m-3\)
\(\Leftrightarrow\left(m-3\right)x< m^2-4m+3\)
\(\Leftrightarrow x< \dfrac{m^2-4m+3}{m-3}=m-1\)
Vậy \(x< m-1\)
Tập nghiệm S của bất phương trình log 1 2 3 x - 2 > log 1 2 4 - x là
A. S = 3 2 ; 4
B. S = - ∞ ; 3 2
C. S = 2 3 ; 3
D. S = 2 3 ; 3 2
Đáp án D
Phương pháp:
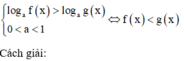
Điều kiện xác đinh:
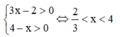
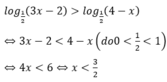
Kết hợp điều kiện xác định, suy ra, bất phương trình có tập nghiệm S = 2 3 ; 3 2
Tập nghiệm S của bất phương trình 5 x + 2 < 1 25 − x là
A. S = − ∞ ; 2
B. S = − ∞ ; 1
C. S = 1 ; + ∞
D. S = 2 ; + ∞
Đáp án D
B P T ⇔ 5 x + 2 < 5 2 x ⇔ x + 2 < 2 x ⇔ x > 2 ⇒ S = 2 ; + ∞
Tập nghiệm S của bất phương trình 5 x + 2 < 1 25 − x là
A. S = 2 ; + ∞
B. S = 1 ; + ∞
C. S = − ∞ ; 1
D. S = − ∞ ; 2
Đáp án A
Ta có:
5 x + 2 < 1 25 − x ⇔ 5 x + 2 < 5 2 x
⇔ x + 2 < 2 x ⇔ x > 2