Tìm tất cả các giá trị của tham số m để phương trình log 2 2 x + log 2 x - m = 0 có nghiệm x ∈ 0 ; 1 .
A. m ≥ 0
B. m ≥ - 1 4
C. m ≥ - 1
D. m ≤ - 1 4
Tất cả các giá trị của tham số m để phương trình log m x = 2 log x + 1 có nghiệm là
![]()
![]()
![]()
![]()
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
Gọi S là tập hợp tất cả các giá trị của tham số m ∈ Z và phương trình:
logmx-5.x2 - 6x + 12= log\(\sqrt{mx-5}\) \(\sqrt{x+2}\) có nghiệm duy nhất. Tính số phần tử của S
ĐKXĐ: \(mx-5>0\) ; \(x>-2\)
\(log_{mx-5}\left(x^2-6x+12\right)=log_{mx-5}\left(x+2\right)\)
\(\Rightarrow x^2-6x+12=x+2\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
TH1: \(x=2\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5>0\\m.5-5< 0\end{matrix}\right.\) \(\Rightarrow\) ktm
TH2: \(x=5\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5< 0\\m.5-5>0\end{matrix}\right.\)
\(\Rightarrow1< m< \dfrac{5}{2}\Rightarrow m=2\)
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
A. 4.
B. 3.
C. 1.
D. 2.
Tìm tất cả các giá trị thực của tham số m để y = l o g ( x 2 - 4 x - m + 1 ) có tập xác định là R
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y= log( x2- 2x- m+ 1) có tập xác định là R
A. m≥ 0.
B. m<0
C. m ≤ 2.
D. m> 2.
Chọn B
Để hàm số đã cho có tập xác định là R khi và chỉ khi : x2- 2x-m+ 1> 0 với mọi x
Hay
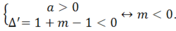
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là R
A. m > -4
B. m < 0
C. m < -4
D. m < -3
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ .
A. m > -4
B. m < 0
C. m < -4
D. m < -3
Chọn D
Hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ khi và chỉ khi
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 2 x - m + 1 ) có tập xác định là R:
A. m ≥ 0
B. m < 0
C. m ≤ 2
D. m > 2