Tìm tất cả các giá trị của tham số m để hàm số y = 1 m l o g 3 2 x - 4 l o g 3 x + m + 3 xác định trên khoảng ( 0 ; + ∞ ) là
A. m ∈ ( - 4 ; 1 )
B. m ∈ [ 1 ; + ∞ )
C. m ∈ ( - ∞ ; - 4 ) ∪ ( 1 ; + ∞ )
D. m ∈ ( 1 ; + ∞ )
Tìm tất cả các giá trị của tham số m để hàm số y = - x 3 + m x 2 - x có 2 điểm cực trị
A. | m | ≥ 2 3
B. | m | > 2
C. | m | > 3
D. | m | ≥ 3
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x + 1 m x − 1 2 + 4 có hai tiệm cận đứng:
A. m < 0
B. m = 0
C. m < 0 m ≠ − 1
D. m < 1
Đáp án là C
Ta có: y = x + 1 m ( x − 1 ) 2 + 4
có hai tiệm cận đứng thì phương trình g(x)= m ( x − 1 ) 2 + 4 phải có 2 nghệm phần biệt khác -1
< = > m ≠ 0 Δ = − 16 m > 0 g ( − 1 ) = 4 m + 4 ≠ 0 < = > m < 0 m ≠ − 1
Tìm tất cả giá trị của m để hàm số y = 1/3.x3 – mx2 + (m2 – m + 1)x + 1 đạt cực đại tại x = 1
A. m = -2
B. m = -1
C. m = 2.
D. m = 1
Đáp án C
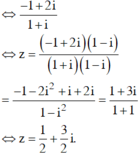
y’’ = 36x2 – 24x – 12
=> y’’(-1) = 48 > 0
Đồ thị hàm số có điểm cực tiểu là M(-1;-10) nên S = -11
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số y = x 4 − 2 x 2 − 2 tại 4 điểm phân biệt là
A. m>-3
B. − 3 < m < − 2
C. − 3 < m < 0
D. 3 < m < 0
Đáp án B
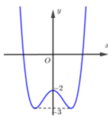
Dựa vào đồ thị hàm số y = x 4 − 2 x 2 − 2
Suy ra − 3 < m < − 2 là giá trị cần tì
Tìm tất cả các giá trị thực của tham số m để hàm số y = log x 2 − 2 m x + 4 có tập xác định là R .
A. m > 2 m < − 2
B. m = 2
C. m < 2
D. − 2 < m < 2
Đáp án D
Để hàm số y = log x 2 − 2 m x + 4 có tập xác định là ℝ thì x 2 − 2 m x + 4 > 0 ∀ x ∈ ℝ
⇔ a = 1 > 0 Δ ' = m 2 − 4 < 0 ⇔ m 2 < 4 ⇔ − 2 < m < 2 .
Tìm tất cả các giá trị của tham số m để phương trình x - 1 l o g 3 ( x + 1 ) = m có hai nghiệm phân biệt
A. -1 < m ≠ 0
B. m > -1
C. không tồn tại m
D. -1 < m < 0
Cho hàm số y=x4−5x2+4 có đồ thị (C). Biết rằng mo là giá trị của tham số m để đường thẳng d:y=m cắt đồ thị (C) tại 4 điểm phân biệt cách đều nhau. Giá trị của mo thuộc khoảng nào sau đây?
Phương trình hoành độ giao điểm: \(x^4-5x^2-m+4=0\)
Đặt \(x^2=t\Rightarrow t^2-5t-m+4=0\) (1)
Gọi 4 hoành độ giao điểm là \(x_1< x_2< x_3< x_4\) và \(t_1< t_2\) là 2 nghiệm dương phân biệt của (1) thì: \(\left\{{}\begin{matrix}x_1=-\sqrt{t_2}\\x_2=-\sqrt{t_1}\\x_3=\sqrt{t_1}\\x_4=-\sqrt{t_2}\end{matrix}\right.\)
Do 4 điểm cách đều \(\Rightarrow x_2-x_1=x_3-x_2\Rightarrow x_1+x_3=2x_2\)
\(\Rightarrow-\sqrt{t_2}+\sqrt{t_1}=-2\sqrt{t_1}\) \(\Rightarrow3\sqrt{t_1}=\sqrt{t_2}\Rightarrow t_2=9t_1\)
\(\Rightarrow\left\{{}\begin{matrix}t_1+t_2=5\\t_2=9t_1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{1}{2}\\t_2=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow-m+4=t_1t_2=\dfrac{9}{4}\)
\(\Rightarrow m=\dfrac{7}{4}\)
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y= (m-3)x- (2m+1).cos x luôn nghịch biến trên R?
A. - 4 ≤ m ≤ 2 3
B. m> 2
C. m > 3 m ≠ 1
D. m<2
Chọn A.
Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx
Hàm số nghịch biến trên R
![]()
Trường hợp 1: m= -1/ 2 ; ta có 0 ≤ 7 2 ∀ x ∈ ℝ
Vậy hàm số luôn nghịch biến trên R.
Trường hợp 2: m< -1/ 2 ; ta có
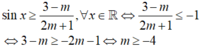
Trường hợp 3:m > -1/2 ; ta có:
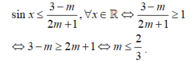
Vậy - 4 ≤ m ≤ 2 3
Cho hàm số y = 1 3 x 3 - 1 2 2 m + 4 x 2 + m 2 + 4 m + 3 x + 1
(m là tham số). Tìm m để
hàm số đạt cực đại tại x 0 = 2
A. m = 1
B. m = - 2
C. m = - 1
D. m = 2