Thể tích lớn nhất của khối trụ nội tiếp hình cầu có bán kính R bằng
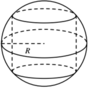
A. 4 πR 3 3 9
B. 8 πR 3 3 3
C. 8 πR 3 27
D. 8 πR 3 3 9
Thể tích lớn nhất của khối trụ nội tiếp hình cầu có bán kính R bằng:
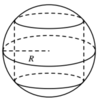
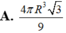
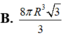
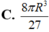
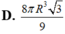
Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là
![]()
![]()
![]()
![]()
Tính chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R .
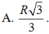
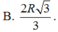
![]()
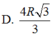
Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là
A. 4 R 3 3
B. R 3
C. R 3 3
D. 2 R 3 3
Gọi d là khoảng cách từ tâm O đến mặt đáy của hình trụ, r là bán kính đáy.
Thể tích khối trụ:
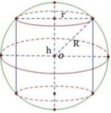
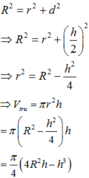
Xét hàm số
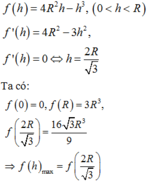
Vậy, thể tích khối trụ lớn nhất khi
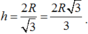
Chọn D
Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là:
A. 4 R 3 3
B. R 3
C. R 3 3
D. 2 R 3 3
Cho mặt cầu (S) có bán kính 3 . Trong tất cả các khối trụ nội tiếp mặt cầu (S) (hai đáy của khối trụ là những thiết diện của hình cầu cắt bởi hai mặt phẳng song song), khối trụ có thể tích lớn nhất bằng bao nhiêu ?
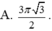
![]()
![]()
![]()
Thể tích khối trụ nội tiếp một mặt cầu có bán kính R không đổi có thể đạt giá trị lớn nhất bằng
A. 4 π 9 3 R 3
B. π 9 3 R 3
C. 2 π 9 3 R 3
D. 4 π 3 9 R 3
Chọn A.
Gọi r, h, V tương ứng là bán kính đáy, chiều cao và thể tích của khối trụ. Ta dễ dàng thấy r 2 + h 2 4 = R 2
Và từ đó
Bây giờ sử dụng bất đẳng thức Cauchy ta có
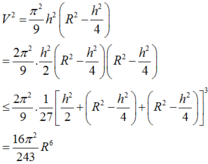
Suy ra V ≤ 4 π 9 3 R 3 . Đẳng thức xảy ra khi và chỉ khi

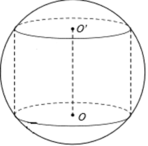
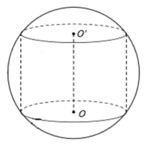
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
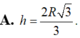
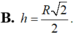
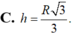
![]()
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
A. h = 2 R 3 3 .
B. h = R 2 2 .
C. h = R 3 3 .
D. h = R 2 .