Cho và Khi đó có giá trị là
A. cos α = - 2 3
B. cos α = 2 2 3
C. cos α = 8 9
D. cos α = - 2 2 3
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
cho cos α=\(\dfrac{1}{3}\).khi đó giá trị biểu thức B=sin(α-\(\dfrac{\Pi}{4}\))-cos\(\left(\text{α}-\dfrac{\Pi}{4}\right)\)là bao nhiêu?
có ai bt làm ko giúp mik với
\(sin\left(\text{α}-\dfrac{\Pi}{4}\right)-cos\left(\text{α}-\dfrac{\Pi}{4}\right)\)
\(=sin\text{α}.cos\dfrac{\Pi}{4}-cos\text{α}-sin\dfrac{\Pi}{4}-\left(cos\text{α}.cos\dfrac{\Pi}{4}+sin\text{α}.sin\dfrac{\Pi}{4}\right)\)
\(=sin\text{α}.\dfrac{\sqrt{2}}{2}-\dfrac{1}{3}.\dfrac{\sqrt{2}}{2}-\dfrac{1}{3}.\dfrac{\sqrt{2}}{2}-sin\text{α}.\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{-2\sqrt{2}}{6}\)
\(=\dfrac{-\sqrt{2}}{3}\)
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
Cho góc nhọn α biết rằng cos α - sin α = 1/3 . Giá trị của sin α .cos α là
A. 2 3
B. 3 2
C. 4 9
D. 9 4
cho cos α=\(\dfrac{1}{3}\).khi đó giá trị biểu thức B=sin\(\left(\alpha-\dfrac{\Pi}{4}\right)-cos\left(\alpha-\dfrac{\Pi}{4}\right)\)
\(B=\sqrt{2}\left(sina-cosa\right)-\sqrt{2}\left(cosa+sina\right)\)
\(=\sqrt{2}\cdot\left(-2cosa\right)=-2\sqrt{2}\cdot\dfrac{1}{3}=-\dfrac{2\sqrt{2}}{3}\)
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Cho góc α thỏa mãn tanα = 2. Tính giá trị biểu thức P = 1 + cos α + cos 2 α sin α + sin 2 α
A. P = 4
B. P = 1/2
C. P = 1
D. P = 1/4
Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
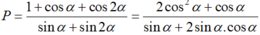
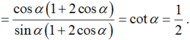
Phương trình dao động của hai dao động điều hòa cùng phương có li độ lần lượt là: x 1 = 3 cos ( πt + 2 π 3 ) (cm) và x 2 = 4 cos ( πt + α ) (cm). Biên độ dao động tổng hợp bằng 5 khi α có giá trị là
A. 105 180 π
B. π 3
C. 7 π 6
D. - π 6
Cho góc α thỏa mãn 0 < α < π 4 v à sin α + cos α = 5 2 . Giá trị của biểu thức P = sin α - cosα là:
A. P = 3 2
B. P = 1 2
C. P = - 1 2
D. P = - 3 2
Chọn D.
Xét biểu thức (sin α - cosα ) 2 + (sin α + cosα ) 2 ta có:
(sin α - cosα ) 2 + (sin α + cosα ) 2
= sin 2 α - 2sin α.cosα + cos 2 α + sin 2 α + 2 sin α.cosα + cos 2 α
= 2( sin 2 α + cos 2 α ) =2
⇒ (sin α - cosα ) 2 = 2 - (sin α + cosα ) 2
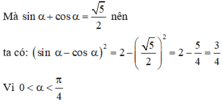
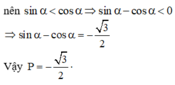
Cho hình chóp tứ giác đều S. ABCD có tất các các cạnh bằng a. Gọi α là góc giữa mặt bên và mặt đáy. Khi đó, cos α nhận giá trị nào sau đây
A. 1 2
B. 6 3
C. 3 3
D. 1 2