Cho hai số thực z 1 , z 2 thỏa mãn z 1 + 5 = 5 và z 2 + 1 - 3 i = z 2 - 3 - 6 i . Tìm giá trị nhỏ nhất của z 1 - z 2
A. 5 2
B. 5 4
C. 10
D. 3
Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và ![]() . Hỏi có bao nhiêu số phức z thỏa mãn
. Hỏi có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Chọn B.
Gọi số phức cần tìm là z = a + bi.
Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)
= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i
+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a
+ ta có ![]() ⇔|a – 2 + (-b + 5)i| = 1
⇔|a – 2 + (-b + 5)i| = 1
Hay ( a - 2) 2 + ( 5 - 3a) 2 = 1
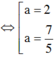 (thỏa mãn)
(thỏa mãn)
Vậy có hai số phức z thỏa mãn là z = 2 + 6i và z = 7/5 + 21/5i
Cho số phức z thỏa mãn \(z^6-z^5+z^4-z^3+z^2-z+1=0\)Tìm phần thực của \(w=z\left(z^2-z+1\right)\)
Cho số phức z thỏa mãn z z ¯ = 1 và z ¯ - 1 = 2 . Tổng phần thực và phần ảo của z bằng
A. -1
B. 0
C. 1
D. 2
Giả sử ![]()
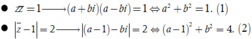
Giải hệ (1) và (2), ta được 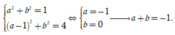
Chọn A.
Cho số phức z thỏa mãn 1 + i z là số thực và |z-2|=m với m ∈ R. Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
A. m 0 ∈ ( 0 ; 1 / 2 )
B. m 0 ∈ ( 1 / 2 ; 1 )
C. m 0 ∈ ( 3 / 2 ; 2 )
D. m 0 ∈ ( 1 ; 3 / 2 )
Tìm số phức z thỏa mãn |z-2|=|z| và (z+1)( z ¯ - i ) là số thực
A. z = 1 + 2 i
B. z = - 1 - 2 i
C. z = 2 - i
D. z = 1 - 2 i
Tìm số phức z thỏa mãn |z-2| = |z| và |z+1|( z ¯ -i) là số thực.
A. z = 1 - 2i
B. z = -1 - 2i
C. z = 2 - i
D. z = 1 + 2i
Đáp án A
Đặt z = a + bi; ![]()
![]()
![]()
Mặt khác ![]()
![]() là số thực, suy ra
là số thực, suy ra
![]()
Tìm số phức z thỏa mãn z - 2 = z và ( z + 1 ) ( z ¯ - i ) là số thực
A. z=1+2i
B. z=-1-2i
C. z=2-i
D. z=1-2i
Đáp án D
Phương pháp.
Gọi ![]() . Sử dụng giả thiết để tìm a, bsuy ra giá trị của z.
. Sử dụng giả thiết để tìm a, bsuy ra giá trị của z.
Lời giải chi tiết.
Giả sử ![]() .Khi đó ta có
.Khi đó ta có
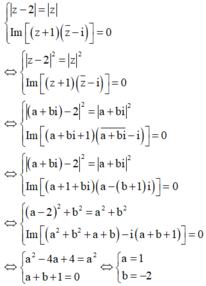
Vậy z=a+bi=1-2i
Sai lầm.Một số học sinh có thể nhớ nhầm i 2 = - 1 thành i 2 = 1 do đó quá trình tính toán kết quả sẽ bị sai.
Tìm số phức z thỏa mãn |z-2| = |z| và (z+1)( z ¯ -i) là số thực.
A. z = 1 - 2i
B. z = -1 - 2i
C. z = 2 - i
D. z = 1 + 2i
Đáp án A
Đặt ![]()
![]()
![]()
Mặt khác ![]()
![]() là số thực, suy ra
là số thực, suy ra
b+2 = 0 ![]()
Biết rằng hai số phức z 1 ; z 2 thỏa mãn z 1 - 3 - 4 i = 1 và z 2 - 3 - 4 i = 1 2 Số phức z có phần thực là a và phần ảo là b thỏa mãn 3a – 2b – 12 = 0. Giá trị nhỏ nhất của P = z - z 1 + z - 2 z 2 + 2 bằng
A. P m i n = 9945 11
B. P m i n = 5 - 2 3
C. P m i n = 9945 13
D. P m i n = 5 + 2 5
Biết rằng hai số phức z 1 , z 2 thỏa mãn z 1 − 3 − 4 i = 1 và z 2 − 3 − 4 i = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a − 2 b − 12 = 0 . Giá trị nhỏ nhất của P = z − z 1 + z − 2 z 2 + 2 bằng:
A. P min = 9945 11 .
B. P min = 5 − 2 3 .
C. P min = 9945 13 .
D. P min = 5 + 2 5 .