Tâm đối xứng của đồ thị hàm số y = 1 + 4 x 1 + x là
A. I(4;-1)
B. I(-1;1)
C. I(4;1)
D. I(-1;4)
Tìm tọa độ tâm đối xứng của đồ thị hàm số y=(2x+1)/(x-1)
A. (1;2)
B. (2;1)
C. (1;-1)
D. (-1;1)
Tọa độ tâm đối xứng của đồ thị hàm số y = x - 2 2 x - 1 là
A. - 1 2 ; 2
B. 1 2 ; 1 2
C. 1 2 ; - 1
D. - 1 2 ; 1 2
Chọn B.
Tâm đối xứng của đồ thị hàm số này là giao điểm của 2 đường tiệm cận 1 2 ; 1 2
Tìm m để tâm đối xứng của đồ thị hàm số C : y = x 3 + m + 3 x 2 + 1 − m trùng với tâm đối xứng của đồ thị hàm số H : y = 14 x − 1 x + 2 .
A. m=2
B. m=1
C. m=3
D. m=0
Đáp án C
Phương pháp: Tâm đối xứng của hàm đa thức bậc ba chính là điểm uốn. Tâm đối xứng của hàm phân thức là giao điểm của các đường tiệm cận.
Cách giải: Đối với hàm số y = 14 x − 1 x + 2 ta thấy T C N : y = 14, T C Đ : x = − 2.
Suy ra tâm đối xứng của đồ thị hàm số (H) là I − 2 ; 14 và I cũng là tâm đối xứng của đồ thị hàm số (C).
Đối với đồ thị hàm số (C) ta có: y ' = 3 x 2 + 2 m + 3 x
⇒ y ' ' = 6 x + 2 m + 3 = 0 ⇔ x = − m + 3 3
Hàm đa thức bậc ba có tâm đối xứng trùng với điểm uốn nên ta có:
− m + 3 3 = − 2 ⇔ m + 3 = 6 ⇔ m = 3
Tâm đối xứng của đồ thị hàm số y = - x 3 - 3 x 2 + 1 là:
A. (-1; -1)
B. (-2; -3)
C. (0; 1)
D. Không có đáp án
y ' = - 3 x 2 - 6 x ; y ' ' = - 6 x - 6 ; y ' ' = 0 = > x = - 1
Vậy điểm U(-1; -1) là tâm đối xứng của đồ thị .
(Đồ thị hàm số bậc ba nhận điểm uốn làm tâm đối xứng – hoành độ điểm uốn là nghiệm phương trình y'' = 0 ).
Chọn đáp án A.
Tâm đối xứng của đồ thị hàm số y = 2 x 3 - 6 x 2 + 3 x + 1
A. (2;-1)
B. (0;1)
C. (-1;-10)
D. (1;0)
Đáp án D
Tâm đối xứng của đồ thị hàm số y = 2 x 3 - 6 x 2 + 3 x + 1 là điểm uốn của đồ thị
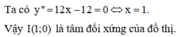
Tâm đối xứng I của đồ thị hàm số y = − 2 x − 1 x + 1 là
A. I 1 ; − 2
B. I − 1 ; − 2
C. I 1 ; 2
D. I − 1 ; 2
Tìm tọa độ tâm đối xứng của đồ thị hàm số y = x 3 - 3 x + 1
A. (-1;4)
B. (0;2)
C. (1;0)
D. đồ thị không có tâm đối xứng
Tìm tọa độ tâm đối xứng của đồ thị hàm số y = x 3 - 3 x + 1
A. (-1;4)
B. (0;2)
C. (1;0)
D. đồ thị không có tâm đối xứng.
Tọa độ tâm đối xứng của đồ thị hàm số y = 3 x - 1 2 x + 1 là
A. ( 1 2 ; 3 2 )
B. ( - 1 2 ; 3 2 )
C. ( 1 2 ; - 3 2 )
D. ( - 1 2 ; 3 2 )
Đáp án là D.
• Đồ thị có tiệm cận đứng và tiệm cận ngang làn lượt là: x = - 1 2 ; y = 3 2
• Giao điểm hai đường tiệm cận là tâm đối xứng của đồ thị hàm số.