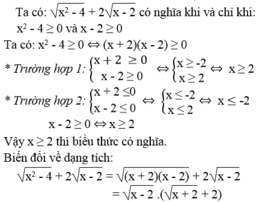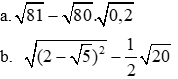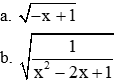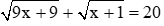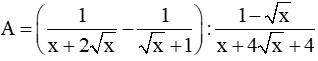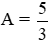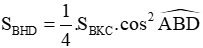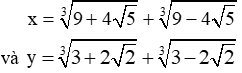Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích: 3 x + 3 + x 2 - 9

Những câu hỏi liên quan
Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích: x 2 - 4 + 2 x - 2
Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích :
a) \(\sqrt{x^2-4}+2\sqrt{x-2}\)
b) \(3\sqrt{x+3}+\sqrt{x^2-9}\)
a. Biểu thức đã cho có nghĩa khi \(\sqrt{x^2-4}\) và \(\sqrt{x-2}\) đồng thời có nghĩa
* \(\sqrt{x^2-4}=\sqrt{\left(x-2\right)\left(x+2\right)}\) có nghĩa khi x \(x\le-2\) hoặc \(x \ge2\)
* \(\sqrt{x-2}\) có nghĩa khi \(x\ge2\)
Vậy điều kiện để biểu thức đã cho có nghĩa là \(x\ge2\)
Với điều kiện trên ta có:
\(\sqrt{x^2-4}+2\sqrt{x-2}=\sqrt{\left(x-2\right)\left(x+2\right)}+2\sqrt{x-2}=\sqrt{x-2}\left(\sqrt{x+2}+2\right)\)
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)
2
a
x
-
2
x
-
3
y
+...
Đọc tiếp
Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)
2 a x - 2 x - 3 y + 3 a y 4 a x + 6 x + 9 y + 6 a y (a là hằng số khác - 3/2
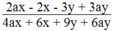 xác định khi 4ax + 6x + 9y + 6ay
≠
0
xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
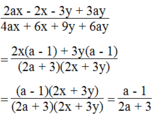
Vậy biểu thức không phụ thuộc vào x, y.
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)
x
2
-
y
2
x
+
y...
Đọc tiếp
Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)
x 2 - y 2 x + y 6 x - 6 y
![]() xác định khi:
xác định khi:
(x + y)(6x – 6y)
≠
0 ⇒ 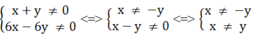
Điều kiện x ≠ ± y
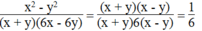
Vậy biểu thức không phụ thuộc vào x, y.
Đúng 0
Bình luận (0)
bài 1:Tìm điều kiện của x để các biểu thức sau có nghãi và biến đổi chúng về dạng tích a) sqrt{x^2-4}+2sqrt{x-2}b) 3sqrt{x+3}+sqrt{x^2-9}bài 2:a) sqrt{x-5}3b) sqrt{x-10} -2c) sqrt{2x-1} sqrt{5}d) sqrt{4-5x}12
Đọc tiếp
bài 1:Tìm điều kiện của x để các biểu thức sau có nghãi và biến đổi chúng về dạng tích
a) \(\sqrt{x^2-4}\)+2\(\sqrt{x-2}\)
b) 3\(\sqrt{x+3}\)+\(\sqrt{x^2-9}\)
bài 2:
a) \(\sqrt{x-5}\)=3
b) \(\sqrt{x-10}\)= -2
c) \(\sqrt{2x-1}\) = \(\sqrt{5}\)
d) \(\sqrt{4-5x}\)=12
Bài 1:
a) \(ĐK:\begin{cases}x^2-4\ge0\\x-2\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x^2\ge4\\x-2\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge2;x\ge-2\\x\ge2\end{cases}\)\(\Leftrightarrow x\ge2\)
\(\sqrt{x^2-4}+2\sqrt{x-2}=\sqrt{\left(x-2\right)\left(x+2\right)}-2\sqrt{x-2}=\sqrt{x-2}\cdot\left(\sqrt{x+2}-2\right)\)
b) \(ĐK;\begin{cases}x+3\ge0\\x^2-9\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-3\\x^2\ge9\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-3\\x\ge3;x\ge-3\end{cases}\)\(\Leftrightarrow x\ge3\)
\(3\sqrt{x+3}+\sqrt{x^2-9}=2\sqrt{x+3}+\sqrt{\left(x-3\right)\left(x+3\right)}=\sqrt{x+3}\left(2+\sqrt{x-3}\right)\)
Đúng 0
Bình luận (0)
baif 2: a) \(\sqrt{x-5}=3\) diều kiện x>=5
pt<=> x-5=9<=>x=14 (thỏa)
b) \(\sqrt{x-10}=-2\) diều kiện x>=10
nhưng ta thầy VT>=0 mà VP<0=> pt trên vô nghiệm
c) \(\sqrt{2x-1}=\sqrt{5}\) diều kiện x>=1/2
pt<=>\(2x-1=5\)<=> x=3(thỏa)
d) \(\sqrt{4-5x}=12\) điều kiện x<=4/5
pt<=> 4-5x=144<=> x=-28 (loại)
Bài 1:a) điều kiện x^2-4>=0 và x-2>=0
<=> x<=-2,x>=2 và x>=2
=> điều kiện là x>=2
b)điều kiện x+3>=0 và x^2-9>=0
<=> x>=-3 và x<=-3, x>=3
=> điều kiện là > x>=3
Đúng 0
Bình luận (0)
Tìm điều kiện x để các biểu thức sau có nghĩa
\(\sqrt{x^2+3}\\ \sqrt{\left(x-1\right)\left(x+2\right)}\)
Để \(\sqrt{x^2+3}\) có nghĩa thì \(x^2+3\ge0\) (luôn đúng)
Để \(\sqrt{\left(x-1\right)\left(x+2\right)}\) có nghĩa thì \(\left(x-1\right)\left(x+2\right)\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x+2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x+2\le0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a) ĐKXĐ: \(x\in R\)
b) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến để các phân thức sau có nghĩa - 5 3 x x - 1 - 2
Tìm điều kiện của các biến để các phân thức sau có nghĩa 2 x 2 + x - 3 x 2 + 5 x + 4
Để phân thức có nghĩa:
x 2 + 5 x + 4 ≠ 0
⇔ (x + 4)(x + 1) ≠ 0
⇔ x ≠ -4, x ≠ -1
Vậy điều kiện để phân thức xác định là x ≠ -4 và x ≠ -1
Đúng 0
Bình luận (0)
Bài 1 (2,0 điểm).1. Thực hiện phép tính. 2. Tìm điều kiện của x để các biểu thức sau có nghĩa: Bài 2 (2,0 điểm).1. Phân tích đa thức thành nhân tử. 2. Giải phương trình: Bài 3 (2,0 điểm. Cho biểu thức: (với x 0; x ≠ 1)a. Rút gọn biểu thức A.b. Tìm x để Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC 8cm, BH 2cm.a. Tính độ dài các đoạn thẳng AB, AC, AH.b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK BH.BC.c. C...
Đọc tiếp
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
2. Giải phương trình:
Bài 3 (2,0 điểm. Cho biểu thức:
(với x > 0; x ≠ 1)
a. Rút gọn biểu thức A.
b. Tìm x để
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a. Tính độ dài các đoạn thẳng AB, AC, AH.
b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
c. Chứng minh rằng:
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 - 3(x + y) + 1993. Tính giá trị biểu thức P với:
Giúp vs ạ 1h nộp cô r
Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)
Đúng 1
Bình luận (0)
x3=18+33√(9+4√5)(9−4√5)(3√9+4√5+3√9−4√5)⇔x3=18+3x3√1⇔x3−3x=18y3=6+33√(3−2√2)(3+2√2)(3√3+2√2+3√3−2√2)⇔y3=6+3y3√1⇔y3−3y=6P=x3+y3−3(x+y)+1993P=(x3−3x)+(y3−3y)+1993P=18+6+1993=2017
Đúng 1
Bình luận (0)