Cho ∫ 0 1 ( 3 x + 3 - 10 ( x + 3 ) 2 ) d x = 3 ln a b - 5 6 , trong đó a, b là 2 số nguyên dương và a b là phân số tối giản. Mệnh đề nào dưới đây đúng ?
![]()
![]()
![]()
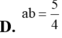
Cho mình hỏi ngu tí:
1/3 = 0,(3)
=> 1/3 x 3 = 0,(3)x 3
1/3 x 3 = 1; 0,(3) x 3 = 0,(9)
=> 1 = 0,(9)
Vì sao lại vậy?
chả biết chỉ thê thôi à phân số và số thập phân khác nhau ở điểm đó cái kỳ diệu là thế tớ chẳng hiểu nổi
1/3 * 3 = 0,(3) * 3
Mà 1/3 * 3 = 1
=>0,(3) * 3 =1
Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
Cho x+y=0 và x;y khác 0.CMR x/(y^3-1) - y/(x^3-1) + 2(x-y)/(x^2y^2+3)=0
tích mình đi
ai tích mình
mình ko tích lại đâu
thanks
tích mình đi
ai tích mình
mình tích lại
thanks
Bài 1 giải các pt sau và diễn tập nghiệm trên trục số a) 2x-6>0 b) -3x+9>0 c)3(x-1)+5>(x+1)+3 d)x/3 - 1/2>x/6 Bài 2:a)cho a>b chứng minh 3a+7>3b+7 b)cho a >b chứng minh a+3>b+1 c) cho 5a -1>5b-1 hãy so sánh a và b Bài 3: 2x(x+5)=0 b) X^2-4=0 d) (x-5)(2x+1)+(x-5)(x+6)=0 Ở bài 1 câu a có dấu hoặc bằng nữa nha bài 2 câu c cũng vậy
3:
a: =>x=0 hoặc x+5=0
=>x=0 hoặc x=-5
b: =>x^2=4
=>x=2 hoặc x=-2
c: =>(x-5)(2x+1+x+6)=0
=>(x-5)(3x+7)=0
=>x=5 hoặc x=-7/3
1.
a. 2x - 6 > 0
\(\Leftrightarrow\) 2x > 6
\(\Leftrightarrow\) x > 3
S = \(\left\{x\uparrow x>3\right\}\)
b. -3x + 9 > 0
\(\Leftrightarrow\) - 3x > - 9
\(\Leftrightarrow\) x < 3
S = \(\left\{x\uparrow x< 3\right\}\)
c. 3(x - 1) + 5 > (x - 1) + 3
\(\Leftrightarrow\) 3x - 3 + 5 > x - 1 + 3
\(\Leftrightarrow\) 3x - 3 + 5 - x + 1 - 3 > 0
\(\Leftrightarrow\) 2x > 0
\(\Leftrightarrow\) x > 0
S = \(\left\{x\uparrow x>0\right\}\)
d. \(\dfrac{x}{3}-\dfrac{1}{2}>\dfrac{x}{6}\)
\(\Leftrightarrow\dfrac{2x}{6}-\dfrac{3}{6}>\dfrac{x}{6}\)
\(\Leftrightarrow2x-3>x\)
\(\Leftrightarrow2x-3-x>0\)
\(\Leftrightarrow x-3>0\)
\(\Leftrightarrow x>3\)
\(S=\left\{x\uparrow x>3\right\}\)
2.
a.
Ta có: a > b
3a > 3b (nhân cả 2 vế cho 3)
3a + 7 > 3b + 7 (cộng cả 2 vế cho 7)
b. Ta có: a > b
a > b (nhân cả 2 vế cho 1)
a + 3 > b + 3 (cộng cả 2 vế cho 3) (1)
Ta có; 3 > 1
b + 3 > b + 1 (nhân cả 2 vế cho 1b) (2)
Từ (1) và (2) \(\Rightarrow\) a + 3 > b + 1
c.
5a - 1 + 1 > 5b - 1 + 1 (cộng cả 2 vế cho 1)
5a . \(\dfrac{1}{5}\) > 5b . \(\dfrac{1}{5}\) (nhân cả 2 vế cho \(\dfrac{1}{5}\) )
a > b
3.
a. 2x(x + 5) = 0
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x+5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(S=\left\{0,-5\right\}\)
b. x2 - 4 = 0
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(S=\left\{0,4\right\}\)
d. (x - 5)(2x + 1) + (x - 5)(x + 6) = 0
\(\Leftrightarrow\left(x-5\right)\left(2x+1+x+6\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(3x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\3x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{-7}{3}\end{matrix}\right.\)
\(S=\left\{5,\dfrac{-7}{3}\right\}\)
(x+5).(x-4)=0
(x-1).(x-3)=0
(3-x).(x-3)=0
x(x+1)=0
tìm x
giải hết mình tick cho
a) (x + 5) (x - 4) = 0
Có 2 TH xảy ra :
TH1 : x + 5 = 0 => x = -5
TH2 : x - 4 = 0 => x = 4
b) (x - 1) (x - 3) = 0
Có 2 TH xảy ra :
TH1 : x - 1 = 0 => x = 1
TH2 : x - 3 = 0 => x = 3
c) (3 - x) (x - 3) = 0
Có 2 TH xảy ra :
TH1 : 3 - x = 0 => x = 3
TH2 : x - 3 = 0 => x = 3
d) x (x + 1) = 0
Có 2 TH xảy ra :
TH1 : x = 0
TH2 : x + 1 = 0 => x = -1
1, xE -5 va 4
2, xE 1 va 3
3, xE 3va 3
4, xE 0
1.Cho x^2+ 4x+1 = 0
Tính A= ( x + 1/x )^2 + (x^2 + 1/x^2 )^2 + ( x^3+ 1/x^3 )^2
2.Cho các số thực x, y khác 0 sao cho x+ 1/y và y+ 1/x là những số nguyên . CMR x^3y^3 + 1/x^3y^3 là số nguyên.
3.Cho x,y,z khác 0 tm x(y+z)^2+y(z+x)^2+z(x+y)^2=4xyz
cho x+y = 1 và xy khác 0. CMR : x/y^3-1 -y/x^3-1 + 2(x-y)/x^2y^2+3=0
Từ giải thiết, ta suy ra được những điều sau :
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}=\frac{x}{\left(y-1\right)\left(y^2+y+1\right)}-\frac{y}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{x}{\left[y-\left(x+y\right)\right]\left(y^2+y+1\right)}-\frac{y}{\left[x-\left(x+y\right)\right]\left(x^2+x+1\right)}\)
\(=\frac{x}{-x\left(y^2+y+1\right)}-\frac{y}{-y\left(x^2+x+1\right)}\)
\(=\frac{-1}{y^2+y+1}+\frac{1}{x^2+x+1}\) (1)
Và \(\left(x^2+x+1\right)\left(y^2+y+1\right)\)
\(=x^2y^2+x^2y+x^2+xy^2+xy+x+y^2+y+1\)
\(=x^2y^2+\left(x^2+xy\left(x+y\right)+xy+y^2\right)+\left(x+y\right)+1\)
\(=x^2y^2+\left(x^2+2xy+y^2\right)+1+1\)
\(=x^2y^2+\left(x+y\right)^2+2\)
\(=x^2y^2+3\) (2)
Từ (1) và (2) suy ra :
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}+\frac{2\left(x-y\right)}{x^2y^2+3}\)
\(=\frac{-1}{y^2+y+1}+\frac{1}{x^2+x+1}+\frac{2\left(x-y\right)}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{-x^2-x-1+y^2+y+1+2x-2y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{-x^2+y^2+x-y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{\left(x+y\right)\left(y-x\right)+x-y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{y-x+x-y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=0\)(ĐPCM)
Biến đổi
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}=\frac{x^4-x-y^4+y}{\left(x^3-1\right)\left(y^3-1\right)}=\frac{\left(x^4-y^4\right)-\left(x-y\right)}{xy\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
(do x+y=1 => y-1=-x và x-1=-y)
\(=\frac{\left(x-y\right)\left(x+y\right)\left(x^3+y^3\right)-\left(x-y\right)}{xy\left(x^2y^2+y^2x+y^2+yx^2+xy+y+x^2+x+1\right)}\)
\(=\frac{\left(x-y\right)\left(x^2+y^2-1\right)}{xy\left[x^2y^2+xy\left(x+y\right)+x^2+y^2+xy+2\right]}\)
\(=\frac{\left(x-y\right)\left(x^2-x+y^2-y\right)}{xy\left[x^2y^2+\left(x+y\right)^2+2\right]}=\frac{\left(x-y\right)\left[x\left(x-1\right)+y\left(y-1\right)\right]}{xy\left(x^2y^2+3\right)}\)
\(=\frac{\left(x-y\right)\left[x\left(-y\right)+y\left(-x\right)\right]}{xy\left(x^2y^2+3\right)}=\frac{\left(x-y\right)\left(-2xy\right)}{xy\left(x^2y^2+1\right)}=\frac{-2\left(x-y\right)}{x^2y^2+3}\)
=> ĐPCM
Cho x + y = 1 và xy = 0
CM: x/y^3-1 + y/x^3-1 + 2(x-y)/x^2y^2+3 =0
Cho x+y=1, xy khác 0. CMR: x/(y^3-1)-y/(x^3-1)+2(x-y)/(x^2y^2+3)=0.
Trả lời nhanh nha các bn, mik đang cần gấp, cảm ơn nhiều.
Kết hợp với giả thiết nêu ra ở đề bài, ta có vài biến đổi sau:
\(\frac{x}{y^3-1}=\frac{x}{\left(y-1\right)\left(y^2+y+1\right)}=\frac{x}{\left[y-\left(x+y\right)\right]\left(y^2+y+1\right)}=-\frac{1}{y^2+y+1}\) \(\left(1\right)\)
\(\frac{y}{x^3-1}=\frac{y}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{y}{\left[x-\left(x+y\right)\right]\left(x^2+x+1\right)}=-\frac{1}{x^2+x+1}\) \(\left(2\right)\)
Mặt khác, ta lại có: \(\left(x^2+x+1\right)\left(y^2+y+1\right)=x^2y^2+xy^2+y^2+x^2y+xy+y+x^2+x+1\)
\(=x^2y^2+\left[x^2+xy\left(x+y\right)+xy+y^2\right]+\left(x+y\right)+1=x^2y^2+\left(x+y\right)^2+2=x^2y^2+3\)
Khi đó, trừ đẳng thức \(\left(1\right)\) cho đẳng thức \(\left(2\right)\) vế theo vế, ta được:
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}=\frac{1}{x^2+x+1}-\frac{1}{y^2+y+1}=\frac{\left(y-x\right)\left(x+y+1\right)}{\left(x^2+x+1\right)\left(y^2+y+1\right)}=\frac{-2\left(x-y\right)}{x^2y^2+3}\)
Vậy, \(\frac{x}{y^3-1}-\frac{y}{x^3-1}+\frac{2\left(x-y\right)}{x^2y^2+3}=-\frac{2\left(x-y\right)}{x^2y^2+3}+\frac{2\left(x-y\right)}{x^2y^2+3}=0\)
Tỷ ơi níu đệ bít thì đệ chết lun
tìm x biết
a) (x+5).(x-4)=0
b) (x-1).(x-3)=0
c) (3-x).(x-3)=0
d) x(x+1)=0
cho mìn cả cách giải với thì mìn T-ick cho 100% là đúng
a) \(\left(x+5\right)\left(x-4\right)=0\)
\(\Rightarrow\hept{\begin{cases}x=-5\\x=4\end{cases}}\)
b) \(\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\hept{\begin{cases}x=1\\x=3\end{cases}}\)
c) \(\left(3-x\right)\left(x-3\right)=0\Rightarrow x=3\)
d) \(x\left(x+1\right)=0\Rightarrow\hept{\begin{cases}x=0\\x=-1\end{cases}}\)
(x+5)(x-4) = 0
\(\orbr{\begin{cases}x+5=0\\x-4=0\end{cases}}\)
\(\orbr{\begin{cases}x=0-5\\x=0+4\end{cases}}\)
\(\orbr{\begin{cases}x=-5\\x=4\end{cases}}\)