Khối đa diện đều có 12 mặt thì có số cạnh là:
A. 30
B. 60
C. 12
D. 24
Những câu hỏi liên quan
Một đa diện đều có số cạnh bằng 30, số mặt bằng 12, đa diện này có số đỉnh là
A. 20
B. 18
C. 40
D. 22
Chọn A
Khối đa diện đều có số mặt bằng 12 là khối thập nhị diện đều.
Khi đó số đỉnh của khối này thỏa 2 C = 3 D ⇔ D = 20 .
*Nhắc lại: Khối đa diện đều loại n , p có C cạnh, M mặt và D đỉnh thì 2 C = n M = p D .
Đúng 0
Bình luận (0)
Một đa diện đều có số cạnh bằng 30, số mặt bằng 12, đa diện này có số đỉnh là
A. 20
B. 18
C. 40
D. 22
Khối đa diện 12 mặt đều có số đỉnh và số cạnh lần lượt là
A. 30 và 20
B. 12 và 20
C. 20 và 30
D. 12 và 30
1. Có thể đặt tương ứng cho mỗi khối đa diện H một số dương VH thỏa mãn các tính chất sau:a) Nếu H là khối lập phương có cạnh bằng một thì VH 1.b) Nếu hai khối đa diện H1 và H2 bằng nhau thì V1 V2.c) Nếu khối đa diện H được phân chia thành hai khối đa diện: H1 và H2 thì VH VH1 + VH2 Số dương VH nói trên được gọi là thể tích của khối đa diện H.Khối lập phương có cạnh bằng một được gọi là khối lập phương đơn vị.Nếu H là khối lăng trụ ABC.A’B’C’ chẳng hạn thì thể tích của nó còn được kí hiệu là...
Đọc tiếp
1. Có thể đặt tương ứng cho mỗi khối đa diện H một số dương VH thỏa mãn các tính chất sau:
a) Nếu H là khối lập phương có cạnh bằng một thì VH =1.
b) Nếu hai khối đa diện H1 và H2 bằng nhau thì V1 = V2.
c) Nếu khối đa diện H được phân chia thành hai khối đa diện: H1 và H2 thì VH = VH1 + VH2 Số dương VH nói trên được gọi là thể tích của khối đa diện H.
Khối lập phương có cạnh bằng một được gọi là khối lập phương đơn vị.
Nếu H là khối lăng trụ ABC.A’B’C’ chẳng hạn thì thể tích của nó còn được kí hiệu là VABC.A’B’C’
2. Thể tích của khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là
V = B.h
Đặc biệt thể tích của khối hộp chữ nhật bằng tích của ba kích thước của nó.
3. Thể tích của khối chóp có diện tích đáy bằng B và chiều cao bằng h là V= 11/3Bh
Kiến thức bổ sung :
4. Cho hình chóp S.ABC. Trên ba tia SA, SB, SC lần lượt lấy ba điểm A’, B’, C’.
Khi đó
5. Nếu H’ là ảnh của H qua một phép dời hình thì
Nếu H’ là ảnh của H qua một phép vị tự tỉ số k thì
6. Bảng tóm tắt của năm loại khối đa diện đều :
| Loại | Tên gọi | Số đỉnh | Số cạnh | Số mặt |
| {3;3} | Tứ diện đều | 4 | 6 | 4 |
| {4;3} | Lập phương | 8 | 12 | 6 |
| {3;4} | Bát diện đều | 6 | 12 | 8 |
| {5;3} | Mười hai mặt đều | 20 | 30 | 12 |
| {3;5} | Hai mươi mặt đều | 12 | 30 | 20 |
Ở đây diện tich toàn phần và thể tích được tính theo cạnh a của đa diện đều.
Xem lại:Bài tập khối đa diện lồi và khối đa diện đều trang 18
B.Giải bài tập sách giáo khoa hình 12 trang 25, 26
Bài 1. (Trang 25 SGK Hình 12 chương 1)
Tính thể tích khối tứ diện đều cạnh a.
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
°
Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện
H
1
và
H
2
trong đó
H
1
chứa điểm C. Thể tích của khối là A. ...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 trong đó H 1 chứa điểm C. Thể tích của khối là
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Đáp án B
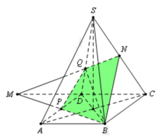
Nối MN cắt SD tại Q, MB cắt AD tại P
Suy ra mp(BMN) cắt khối chóp S.ABCD theo thiết diện tứ giác BPQN và chia khối chóp thành 2 đa diện
Đúng 0
Bình luận (0)
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc
60
∘
. Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V A.
V
7
6
a
3
36
B.
V...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc 60 ∘ . Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V
A. V = 7 6 a 3 36
B. V = 7 6 a 3 72
C. V = 5 6 a 3 72
D. V = 5 6 a 3 36
Đáp án C
Ta có: 2 O D 2 = a 2 ⇒ O D = a 2
⇒ S O = O D tan 60 ∘ = a 2 . 3 = a 3 2
Gọi H là hình chiếu của N lên (ABCD) là trung điểm của OC.
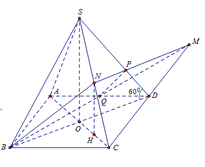
Ta có: N H = S O 2 = a 6 4 ; S M B C = S A B C D = a 2
V N . B C M = 1 3 N H . S M B C = 1 3 . a 6 4 . a 2 = a 3 6 12
Ta có:
M D D C . C S C N . N P P M = 1 ⇔ 1.2. N P P M = 1 ⇔ N P P M = 1 2 ⇒ P M M N = 2 3
Ta có: V M . D P Q V M . B C N = P M M N . M D M C . M Q M B = 2 3 . 1 2 . 1 2 = 1 6
⇒ V N p Q D C A = 5 6 V N . B C M = 5 6 . a 3 6 12 = 5 a 3 6 72
Đúng 0
Bình luận (0)
Hãy khoanh vào chữ cái đặt trước câu trả lời đúng nhất: Câu 1: Không mét khối, sáu phần trăm mét khối được viết là: A. 0,6 m3 B. 0,006m3 C. 0,06m3 D. 0,600m3 Câu 2: 1giờ 40phút ... ? A. 1,40 giờ B. 140 phút C. 100 phút D. giờ Câu 3: Thể tích hình hộp chữ nhật có chiều dài 3,6cm, chiều rộng 2cm và chiều cao 1,2cm: A. 6,72cm3 B. 6,8cm3 C. 8,64 cm3 D. 9cm3 Câu 4: Diện tích của hình tròn có bán kính r 6cm là: A. 113,4cm2 B. 113,04cm2 C. 18,84cm2 D. 13,04cm2 Câu 5: Hình lập phương là hình:...
Đọc tiếp
Hãy khoanh vào chữ cái đặt trước câu trả lời đúng nhất: Câu 1: Không mét khối, sáu phần trăm mét khối được viết là: A. 0,6 m3 B. 0,006m3 C. 0,06m3 D. 0,600m3 Câu 2: 1giờ 40phút = ... ? A. 1,40 giờ B. 140 phút C. 100 phút D. giờ Câu 3: Thể tích hình hộp chữ nhật có chiều dài 3,6cm, chiều rộng 2cm và chiều cao 1,2cm: A. 6,72cm3 B. 6,8cm3 C. 8,64 cm3 D. 9cm3 Câu 4: Diện tích của hình tròn có bán kính r = 6cm là: A. 113,4cm2 B. 113,04cm2 C. 18,84cm2 D. 13,04cm2 Câu 5: Hình lập phương là hình: A. Có 6 mặt đều là hình vuông, có 8 đỉnh và 12 cạnh bằng nhau B. Có 6 mặt đều là hình chữ nhật, có 8 đỉnh và 12. C. Có 6 mặt đều là hình chữ nhật, có 12 đỉnh và 8 cạnh. D. Có 6 mặt đều là hình vuông, có 12 đỉnh và 8 cạnh bằng nhau Câu 6: Số thích hợp để điền vào chỗ chấm: 0,22 m3 = ... dm3 là: A. 22 B. 220 C. 2200 D. 22000 Câu 7: Diện tích toàn phần của hình lập phương có cạnh 2cm là: A. 24cm2 B. 16cm2 C. 42cm2 D. 20cm2 Câu 8: Tìm số tự nhiên x, biết : 64,97 < x < 65,14. Vậy x bằng : A. 64 B. 65 C. 66 D. 63
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng
60
°
. Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện
H
1
và
H
2
, trong đó
H
1
chứa điểm C. Thể t...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° . Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 , trong đó H 1 chứa điểm C. Thể tích của khối H 1 là:
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A B C là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA2/3. Mặt phẳng (SA B ) chia khối đa diện đã cho thành hai phần. Gọi
V
1
là thể tích phần khối đa diện chứa đỉnh A,
V
2
là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng A.
72
V
1...
Đọc tiếp
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A' B' C' là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA=2/3. Mặt phẳng (SA' B' ) chia khối đa diện đã cho thành hai phần. Gọi V 1 là thể tích phần khối đa diện chứa đỉnh A, V 2 là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng
A. 72 V 1 = 5 V 2
B. 3 V 1 = V 2
C. 24 V 1 = 5 V 2
D. 4 V 1 = 5 V 2
