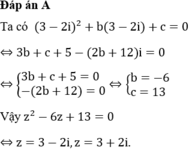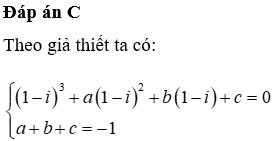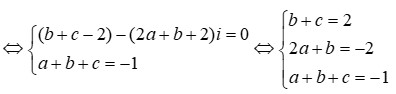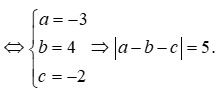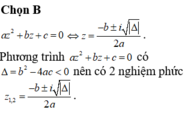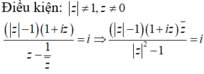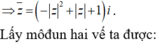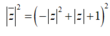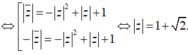Phương trình z 2 + b z + c ( b , c ∈ R , c > 0 ) có hai nghiệm phức z 1 , z 2 và M,N lần lượt là điểm biểu diễn các số phức z 1 , z 2 . Biết rằng tam giác OMN đều. Mệnh đề nào dưới đây đúng ?
A. b 2 = 3 c .
B. b 2 = 2 c .
C. b 2 = 5 c .
D. b 2 = 6 c .