Số mặt phẳng đối xứng của khối tứ diện đều là
A. 7
A. 7
C. 9
D. 6
Cho khối tứ diện đều ABCD cạnh a. Gọi E là điểm đối xứng của A qua D. Mặt phẳng qua CE và vuông góc với mặt phẳng (ABD) cắt cạnh AB tại điểm F. Tính thể tích V của khối tứ diện AECF.
A. V = 2 a 3 30 .
B. V = 2 a 3 60 .
C. V = 2 a 3 40 .
D. V = 2 a 3 15 .
Cho khối tứ diện đều ABCD cạnh a. Gọi E là điểm đối xứng của A qua D. Mặt phẳng qua CE và vuông góc với mặt phẳng (ABD) cắt cạnh AB tại điểm F. Tính thể tích V của khối tứ diện AECF.
A. V = 2 a 3 30
B. V = 2 a 3 60
C. V = 2 a 3 40
D. V = 2 a 3 15
Cho khối tứ diện đều ABCD cạnh a. Gọi E là điểm đối xứng của A qua D. Mặt phẳng qua CE và vuông góc với mặt phẳng (ABD) cắt cạnh AB tại điểm F. Tính thể tích V của khối tứ diện AECF.
A. 2 a 3 30
B. 2 a 3 60
C. 2 a 3 40
D. 2 a 3 15
Đáp án D
Gọi G là trọng tâm tam giác ABD
![]()
![]()
=> (CEF) là mặt phẳng cần dựng.
Ta tính được
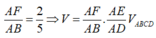
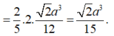
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 6
B. 7
C. 9
D. 9
Đáp án A
Tứ diện đều có 6 mặt phẳng đối xứng đó là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối diện
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 6
B. 7
C. 9
D. 10
Đáp án A
Tứ diện đều có 6 mặt phẳng đối xứng đó là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối diện
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 7
B. 8
C. 9
D. 6
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 7
B. 8
C. 9
D. 6
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E là điểm đối xứng của A qua D. Mặt phẳng qua CE và vuông góc với mặt phẳng A B D cắt cạnh AB tại điểm F. Thể tích của khối tứ diện AECF bằng
A. 2 a 3 15
B. 2 a 3 30
C. 2 a 3 40
D. 2 a 3 60
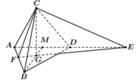
Gọi G là trọng tâm tam giác ABD suy ra C G ⊥ A B D
Do đó mặt phẳng cần dựng là (CEG). Gọi F = E G ∩ A B

Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V .
A. 7 2 a 3 216
B. 11 2 a 3 216
C. 13 2 a 3 216
D. 2 a 3 18