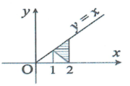
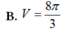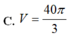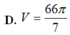Tính thể tích của miền phẳng D (phần gạch chéo ở hình vẽ) khi cho D quay quanh trục Ox
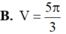
![]()
![]()
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x cung tròn có phương trình y = 6 - x 2 ( 6 ≤ x ≤ 6 ) và trục hoành (phần gạch chéo trong hình vẽ). Tính thể tích V của vật thể xoay tròn sinh bởi hình phẳng D khi quay D quanh trục Ox.
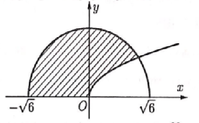
A. V = 8 π 6 - 2 π .
B. V = 8 π 6 + 22 π 3 .
C. V = 8 π 6 - 22 π 3 .
D. V = 4 π 6 + 22 π 3 .
Cho hình phẳng H (phần gạch chéo trong hình vẽ). Thể tích khối tròn xoay tạo thành khi quay hình H quanh trục Ox được tính theo công thức nào dưới đây?
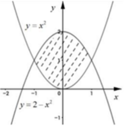
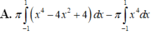
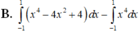

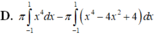
Đáp án A
Thể tích vật thể tạo thành khi quay phần hình phẳng giới hạn bởi hai đồ thị hàm số y = f (x) ; y = g (x) và
hai đường thẳng x = a; x = b quanh trục Ox là V = π ∫ a b f 2 x - g 2 x d x
Cách giải:
Ta có :
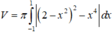
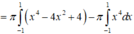
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
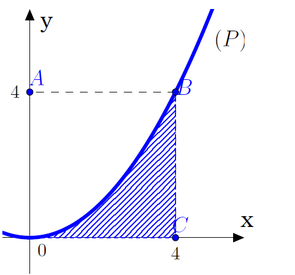
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
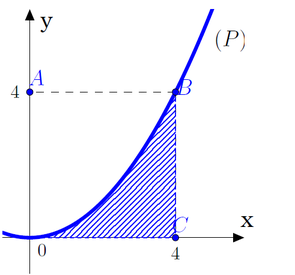
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
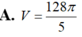
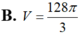
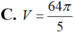
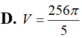
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ).
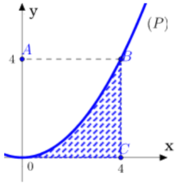
Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
A. V = 128 π 5
B. V = 128 π 3
C. V = 64 π 5
D. V = 256 π 5
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
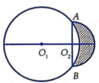
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
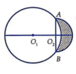
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Đáp án C

Chọn hệ tọa độ Oxy như hình vẽ với O 3 ≡ O , O 2 C ≡ O x , O 2 A ≡ O y .
Ta có
O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4 ⇒ O 1 − 4 ; 0 .
Phương trình đường tròn O 1 : x + 4 2 + y 2 = 25.
Phương trình đường tròn O 2 : x 2 + y 2 = 9.
Kí hiệu H 1 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x = 0 khi x ≥ 0 .
Kí hiệu H 2 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x=0 khi x ≥ 0 .
Khi đó thể tích V cần tìm chíình bằng thể tích V 2 của khối tròn xoay thu được khi quay hình H 2 xung quanh trục Ox (thể tích nửa khối cầu bán kính bằng 3) trừ đi thể tích V 1 của khối tròn xoay thu được khi quay hình H 1 xung quanh trục Ox.
Ta có V 2 = 1 2 . 4 3 π 3 3 = 18 π (đvtt);
V 1 = π ∫ 0 1 y 2 d x = π ∫ 0 1 25 − x + 4 2 d x = 14 π 3 (đvtt).
Vậy V = V 2 − V 1 = 18 π − 14 π 3 = 40 π 3 (đvtt).
Cho (H) là hình phẳng giới hạn bởi 1 4 cung tròn có bán kính R=2, đường cong y = 4 - x và trục hoành ( miền tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.