Xác định a>0 sao cho diện tích giới hạn bởi hai parabol: y = 4 a 2 - 2 ax - x 2 1 + a 4 , y = x 2 1 + a 4 có giá trị lớn nhất.
A.![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong hệ trục tọa độ Oxyz, cho Parabol P : y = x 2 và hai đường thẳng y = a , y = b 0 < a < b (hình vẽ). Gọi S 1 là diện tích hình phẳng giới hạn bởi parabol (P) đường thẳng y = a và đường thẳng y = b (phần gạch chéo) và S 2 là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng y = a (phần tô đậm). Với điều kiện nào sau đây của a và b thì S 1 = S 2
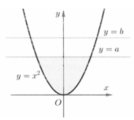
A. b = 4 a 3
B. b = 2 a 3
C. b = 3 a 3
D. b = 6 a 3
Cho parabol P 1 : y = - x 2 + 2 x + 3 cắt trục hoành tại hai điểm A, B và đường thẳng d : y = a 0 < a < 4 . Xét parabol P 2 đi qua A, B và có đỉnh thuộc đường thẳng y = a . Gọi S 1 là diện tích hình phẳng giới hạn bởi P 1 và d. S 2 là diện tích hình phẳng giới hạn bởi P 2 và trục hoành. Biết S 1 = S 2 , tính T = a 3 - 8 a 2 + 48 a .
A. T = 99
B. T = 64
C. T = 32
D. T = 72
Chọn đáp án B
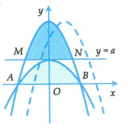
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị. Khi đó, phương trình các parabol mới là
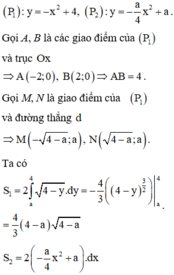
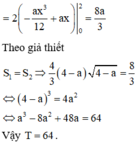
Cho Parabol P : y = x 2 và hai điểm A, B thuộc P sao cho A B = 2 . Diện tích hình phẳng giới hạn bởi P và đường thẳng AB đạt giá trị lớn nhất bằng bao nhiêu?
A. 4 3
B. 5 3
C. 2 3
D. 5 4
Diện tích hình phẳng giới hạn bởi hai parabol y = 1 2 x 2 và y = 6 - x 2 bằng
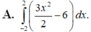
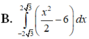
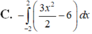
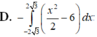
Chọn đáp án C.
Phương trình hoành độ giao điểm:
![]()
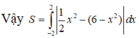
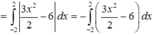
Diện tích hình phẳng giới hạn bởi hai parabol y = 1 2 x 2 và y = 6 - x 2 bằng
A. ∫ - 2 2 3 x 2 2 - 6 d x
B. ∫ - 2 3 2 3 x 2 2 - 6 d x
C. ∫ - 2 2 3 x 2 2 - 6 d x
D. ∫ - 2 3 2 3 x 2 2 - 6 d x
Cho parabol P ; y = x 2 và một đường thẳng d thay đổi cắt (P) tại hai điểm A, B sao cho AB = 2018. Gọi S là diện tích hình phẳng giới hạn bởi (P) và đường thẳng d. Tìm giá trị lớn nhất S m a x của S.
A. S m a x = 2018 3 6
B. S m a x = 2018 3 3
C. S m a x = 2018 3 - 1 6
D. S m a x = 2018 3 + 1 3
Chọn đáp án A
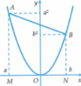
Giả sử A a ; a 2 và B b ; b 2 là hai điểm thuộc (P) và thỏa mãn AB = 2018.
Phương trình đường thẳng d đi qua hai điểm A và B là
![]()
![]()
Diện tích hình phẳng giới hạn bởi (P) và đường thẳng d là:
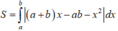
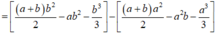
= 1 6 b - a 3
Gọi M là hình chiếu của A trên Ox và N là hình chiếu của B trên Ox. Suy ra M(a;0) và N(b;0).
Ta luôn có M N ≤ A B hay b - a = b - a ≤ 2018 .
Dấu “=” xảy ra khi MN//AB hay AB//Ox. Khi đó a = -1009; b = 1009.
Vậy S = 1 6 b - a 3 = 2018 3 6
Cho a là số thực dương, gọi S là diện tích hình phẳng giới hạn bởi hai parabol P 1 : y = x 2 1 + a 4 và P 2 : y = 4 a 2 - 2 a x - x 2 1 + a 4 . Tìm giá trị lớn nhất của S.
A. maxS=9
B. m a x S = 27 4
C. m a x S = 9 27 4 4
D. m a x S = 9 4
Cho hàm số y = f x liên tục, xác định trên đoạn a ; b . Diện tích hình phằng giới hạn bởi đồ thị hàm số y = f x , trục hoành và hai đường thẳng x = a , x = b được tính theo công thức.
A. S = ∫ a b f x d x
B. S = ∫ a b f x d x
C. S = - ∫ a b f x d x
D. S = - ∫ a b f x d x
Chọn A.
Phương pháp: Theo công thức tính diện tích hình phẳng.
Cách giải: Chọn A.
Cho (H) là hình phẳng giới hạn bởi Parabol y = 3 x 2 , cung tròn có phương trình y = 4 - x 2 0 ≤ x ≤ 2 và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
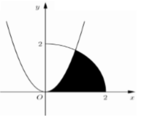
A. 4 π + 3 12
B. 4 π - 3 6
C. 4 π + 2 3 - 3 6
D. 5 3 - 2 π 3