Xét các số thực c > b > a > 0 . Cho hàm số y = f x có đạo hàm liên tục trên ℝ và có bảng xét dấu của đạo hàm như hình vẽ. Đặt g x = f x 3 . Số điểm cực trị của hàm số y = g x là
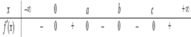
![]()
![]()
![]()
![]()
Xét các số thực x>b>a>0. Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ. Đặt g x = f x 3 Số điểm cực trị của hàm số y=g(x) là
![]()
A. 3
B. 7
C. 4
D. 5
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho hàm số y = f(x) có đạo hàm liên tục trên R, đồ thị của hàm số y = f′(x) như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(x) = f(0) trên đoạn [−3;6] là
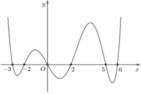
A. 4
B. 3.
C. 5.
D. 2.
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1
Cho hàm số y = f(x) liên tục trên ℝ với bảng xét dấu đạo hàm như sau

Hỏi hàm số y = f(x) có bao nhiêu điểm cực trị?
A. 0
B. 1
C. 2
D. 3
Nhận thấy y' đổi dấu khi qua x = -3 và x = 2 nên hàm số có 2 điểm cực trị. ( x = 1 không phải là điểm cực trị vì y' không đổi dấu khi qua x = 1). Chọn C.
Cho hàm số y=f( x ) có đạo hàm liên tục trên ℝ và có đồ thị của hàm y= f ' ( x ) như hình vẽ
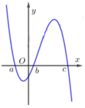
Xét hàm số ![]() Mệnh đề nào dưới đây sai?
Mệnh đề nào dưới đây sai?
A. Hàm số f (x) đạt cực đại tại x=2
B. Hàm số f (x) nghịch biến trên - ∞ ; 2
C. Hàm số f(x) đồng biến trên ( 2; + ∞ )
D. Hàm số f(x) đồng biến trên ( -1; 0)
Đáp án D
Dễ thấy 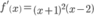
Do f (x) đổi dấu từ âm sang dương khi qua điểm x = 2 nên f (x) đạt cực trị tại x =2
Hàm số f (x) nghịch biến trên do 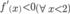
Đặt 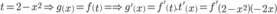
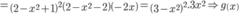
đồng biến trên 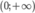
Cho hàm số y= f(x) liên tục trên ℝ và có bảng xét dấu của đạo hàm như hình vẽ.
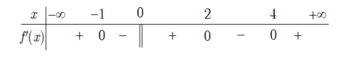
Hàm số y= f(x) có bao nhiêu điểm cực trị?
A. 4.
B. 1.
C. 2.
D. 3.