Cho hình hộp đứng A B C D . A 1 B 1 C 1 D 1 có đáy ABCD là hình vuông cạnh 2a, đường thẳng D B 1 tạo với mặt phẳng ( B C B 1 C 1 ) góc 30 o . Tính thể tích khối hộp A B C D . A 1 B 1 C 1 D 1
A. a 3 3
B. a 3 2 3
C. 8 a 3 2
D. a 3
Cho biết mệnh đề nào sau đây là đúng?
a) Hình hộp là hình lăng trụ đứng
b) Hình hộp chữ nhật là hình lăng trụ đứng
c) Hình lăng trụ là hình hộp
d) Có hình lăng trụ không phải là hình hộp
a sai, b đúng, c sai, d đúng
Hình hộp là hình lăng trụ tứ giác có đáy là hình bình hành
Cho hình hộp chữ nhật ABCDA'B'C'D. Tại đỉnh A có một con sâu, mỗi lần di chuyển, nó bò theo cạnh của hình hộp chữ nhật và đi đến đỉnh kề với đỉnh nó đang đứng. Tính xác suất sao cho sau 9 lần di chuyển, nó đứng tại đỉnh C'.
Hình hộp đứng ABCD.A′B′C′D′ có đáy là hình thoi. Diện tích các tứ giác ABCD,ACC′A′,BDD′B′ lần lượt là S 1 , S 2 , S 3 . Khi đó thể tích khối hộp ABCD.A′B′C′D′ là
A. 1 3 S 1 S 2 S 3
B. 1 2 S 1 S 2 S 3
C. 1 3 S 1 S 2 S 3
D. 1 2 S 1 S 2 S 3
Cho hình hộp đứng ABCD.A¢B¢C¢D¢ có AB = a, AD = 2 a , BD = a 3 . Góc tạo bởi AB¢ và mặt phẳng (ABCD) bằng 60 o . Tính thể tích của khối chóp D¢.ABCD.
A. 3 3 a 3 .
B. 3 a 2 .
C. a 3 .
D. 2 3 3 a 3 .
Cho hình hộp đứng ABCD.A' B' C' D' có đáy là hình thoi, AC = 6a, BD = 8a. Chu vi của một đáy bằng 4 lần chiều cao của khối hộp. Thể tích của khối hộp ABCD.A' B' C' D' là:
A. 240 a 3
B. 120 a 3
C. 40 a 3
D. 80 a 3
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).
a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).
b) Tính thể tích của khối hộp.
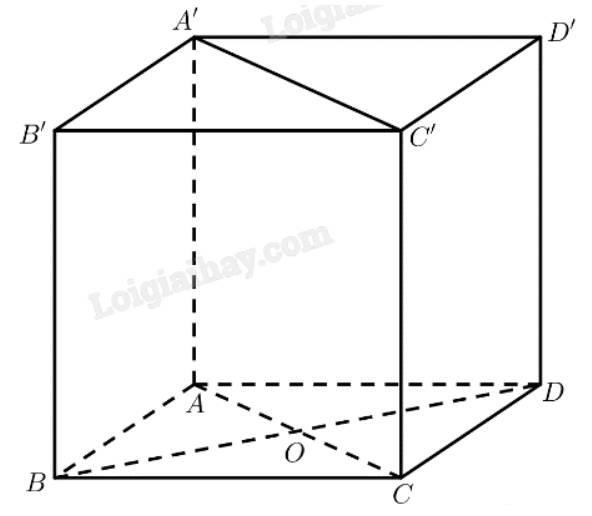
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi. Cho biết \(AB = BD = a,A'C = 2a\).
a) Tính độ dài đoạn thẳng \(AA'\).
b) Tính tổng diện tích các mặt của hình hộp.
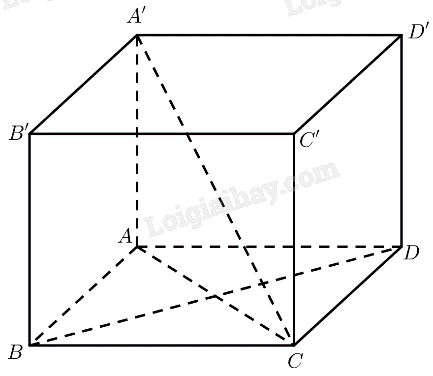
a) Xét tam giác \(AB{\rm{D}}\) có: \(AB = A{\rm{D}} = B{\rm{D}} = a\)
\( \Rightarrow \Delta AB{\rm{D}}\) đều \( \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ } \Rightarrow \widehat {ABC} = {180^ \circ } - \widehat {BA{\rm{D}}} = {120^ \circ }\)
Xét tam giác \(AB{\rm{C}}\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC} = a\sqrt 3 \)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow AA' = \sqrt {A'{C^2} - A{C^2}} = a\)
b) Ta có:
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = {S_{A'B'C'D'}} = AB.AC.\sin \widehat {BAC} = \frac{{{a^2}\sqrt 3 }}{2}\\{S_{ABB'A'}} = {S_{C{\rm{DD}}'{\rm{C}}'}} = AB.AA' = {a^2}\\{S_{A{\rm{DD}}'A'}} = {S_{BCC'B'}} = A{\rm{D}}.AA' = {a^2}\end{array}\)
Tổng diện tích các mặt của hình hộp là:
\(S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'D'}} + {S_{ABB'A'}} + {S_{C{\rm{DD}}'{\rm{C}}'}} + {S_{A{\rm{DD}}'A'}} + {S_{BCC'B'}} = 2.\frac{{{a^2}\sqrt 3 }}{2} + 4.{a^2} = \left( {4 + \sqrt 3 } \right){a^2}\)
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’
a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Diện tích xung quanh:
2 x 3 x (5+7)= 72(cm2)
Thể tích của HHCN:
3 x 5 x 7 = 105(cm3)
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’ a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Sxq=(5+7)*2*3=6*12=72cm2
V=5*7*3=105cm3
Cho hình hộp ABCD.A'B'C'D' biết A(1; 0; 1), B(2; 1; 2), D(1; -1; 1), C'(4; 5; -5). Tính tọa độ các đỉnh còn lại của hình hộp.