Trong không gian cho 3 điểm A(1;0;0), B(0;0;1) và C(2;1;1). Diện tích của tam giác ABC là
A. 6 2
B. 5 2
C. 10 2
D. 15 2
Trong không gian Oxyz, cho hai điểm A(5;1;3), H(3;-3;-1). Tọa độ của điểm A' đối xứng với A qua H là:
A. (-1;7;5)
B. (1;7;5)
C. (1;-7;-5)
D. (1;-7;5).
Đáp án C
Do A' đối xứng với A qua H nên AA' nhận H làm trung điểm
=> xA' = 2xH-xA = 1; yA' = 2yH-yA = -7; zA' = 2zH-zA = -5.
Trong không gian Oxyz, cho hai điểm A(1;2;−3) và B(3; −2; −1). Tọa độ trung điểm đoạn thẳng AB là điểm
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm A(2; 0; 1), B(-1; 2; 3). Tính khoảng cách giữa hai điểm AB
A. A B = 17
B. A B = 13
C. A B = 14
D. A B = 19
Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; 1; -3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
A . M 3 2 ; 1 2 ; 0
B . M 1 2 ; - 3 2 ; 0
C. M (0; 0; 5)
D. M (3; -4; 0)
Trong không gian Oxyz, cho 2 điểm A(2;-1;-3), B(0;3;-1). Phương trình đường kính AB là
A. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 6
B. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 24
C. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 24
D. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 6
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB = 2/3. Khi đó độ dài OM lớn nhất bằng:
A. 6 3
B. 12 3
C. 5 3 2
D. 5 3
Chọn B
Gọi M (x; y; z)
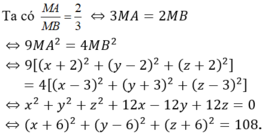
Như vậy, điểm M thuộc mặt cầu (S) tâm I(-6;6;-6) và bán kính R = √108 = 6√3. Do đó OM lớn nhất bằng
![]()
Trong không gian Oxyz cho hai điểm A(1;-1;-3) và B(-2;1;-1). Độ dài đoạn thẳng AB bằng
A. 17
B. 5
C. 13
D. 3
Trong không gian Oxyz, cho hai điểm A(1;−2;1), B(0;1;−3). Toạ độ véctơ A B ⇀ là
A. (1;-3;4)
B. (1;-1;2)
C. (-1;3;-4)
D. (-1;1;2)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1 ;2 ;3) và B(3 ;-1 ;2). Điểm M thỏa mãn M A . M A → = 4 M B . M B → có tọa độ là:
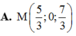
![]()
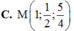
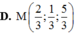
Trong không gian Oxyz, cho 2 điểm A(2;-1;-3), B(0;3;-1). Phương trình mặt cầu đường kính AB là
A. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 6
B. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 24
C. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4
D. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 6