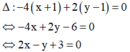Cho số phức z thỏa mãn z - 3 + z + 3 = 8 . Gọi M, m lần lượt giá trị lớn nhất và nhỏ nhất z Khi đó M + m bằng
A. 4 - 7
B. 4 + 7
C. 7
D. 4 + 5
Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i
A. W=-4+8i
B. w=1=3i
C. w= -1+7i
D. w=-3+8i
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z thỏa mãn z + ( 2 + i ) z ¯ = 3 + 5 i . Tính môđun của số phức z.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
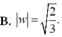
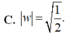
![]()
Cho số phức z thỏa mãn z + 2 + i z ¯ = 3 + 5 i . Tính môđun của số phức z
A. z = 13
B. z = 5
C. z = 13
D. z = 5
Cho số phức z thỏa mãn ( 3 + i ) z - i z = 7 - 6 i . Môđun của số phức z bằng
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn (3 + i).z - i.z =7 - 6i Mô đun của số phức z bằng:
A. 25
B. 2 5
C. 5
D. 5
Cho số phức z thỏa mãn z - 1 + 2 i = 3 . Tìm môđun lớn nhất của số phức z - 2 i
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z - 4 + 3 i - z ¯ + 4 + 3 i = 10 và z - 3 - 4 i nhỏ nhất. Môđun của số phức z bằng
A. 6
B. 7
C. 5
D. 8
Cho số phức z thỏa mãn điều kiện: z − 1 = z + 3 − 2 i . Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng
B. Đường tròn
C. Một điểm xác định
D. Elip
Đáp án A
Em hãy thực hiện câu này theo cả 2 cách nhé!
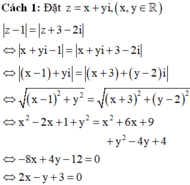
Vậy tập hợp các điểm biểu diễn số phức z là một đường thẳng có phương trình: 2x - y + 3 = 0
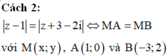
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
AB → = − 4 ; 2 , trung điểm của AB là I − 1 ; 1 , ∆ qua điểm I nhận AB → = − 4 ; 2 làm vectơ pháp tuyến.