Với một chất xác định hệ số nở dài và hệ số nở khối có mối liên hệ
A. β = 2 α
B. β = α 3
C. α = 1 3 α
D. β = α 1 2
Giữa hệ số nở khối β và hệ số nở dài α có biểu thức:
A. β = α 3
B. β = 3 α
C. β = α 3
D. β = 3 α
Giữa hệ số nở khối β và hệ số nở dài α có biểu thức:
A. β = α 3
B. β = 3 α
C. β = α 3
D. β = 3 α
Giữa hệ số nở khối β và hệ số nở dài α có biểu thức:
A. β = α 3
B. β = 3 α
C. β = α 3
D. β = 3 α
Giữa hệ số nở khối β và hệ số nở dài α có biểu thức:
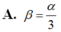
![]()
![]()
![]()
Đáp án: D
Sự nở vì nhiệt của vật rắn là sự tăng kích thước của vật rắn khi nhiệt độ tăng do bị nung nóng.
+ Độ nở dài của vật rắn tỉ lệ thuận với độ tăng nhiệt độ Dt và độ dài ban đầu l0 của vật đó:
Dl = l – l0 = al0Dt.
+ Độ nở khối của vật rắn tỉ lệ thuận với độ tăng nhiệt độ Dt và thể tích ban đầu V0 của vật đó:
DV = V – V0 = bV0Dt; với b » 3a.
Giữa hệ số nở khối β và hệ số nở dài α có biểu thức:
A. β = α 3
B. β = 3 α
C. β = α 3
D. β = 3 α
Chọn D
Sự nở vì nhiệt của vật rắn là sự tăng kích thước của vật rắn khi nhiệt độ tăng do bị nung nóng.
Xét một vật rắn đồng chất, đẳng hướng và có dạng khối lập phương. Hãy chứng minh độ tăng thể tích ΔV của vật rắn này khi bị nung nóng từ nhiệt độ đầu to đến nhiệt độ t được xác định bởi công thức :
ΔV = V - Vo = βVoΔt
Với Vo và V lần lượt là thể tích của vật rắn ở nhiệt độ đầu to và nhiệt độ cuối t, Δt = t - to, β ≈ 3α (α là hệ số nở dài của vật rắn này).
Chú ý: α2 và α3 rất nhỏ so với α.
Ở nhiệt độ t0 (ºC) cạnh hình lập phương là l0
→ thể tích khối lập phương là:
Ở nhiệt độ t (ºC) cạnh hình lập phương là l
→ thể tích khối lập phương là: V = l3
Mặt khác ta có: l = l0.(1 + αΔt) ⇒ V = l03.(1 + αΔt)3
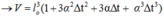
Do α rất nhỏ nên α2 và α3 cũng rất nhỏ, ta có thể bỏ qua.
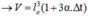
→ ΔV = V – V0 = V0.β.Δt
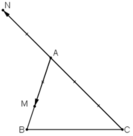
Cho tam giác ABC và hai điểm M, N sao cho A M → = α A B → v à A N → = β A C →
a) Hãy vẽ M, N khi α = 2 3 v à β = - 2 3
b) Tìm mối liên hệ giữa α và β để MN song song với BC.
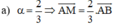
Vậy 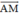 là vec tơ cùng hướng với
là vec tơ cùng hướng với 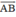 và có độ dài
và có độ dài 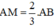
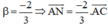
Vậy 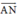 là vec tơ ngược hướng với
là vec tơ ngược hướng với 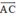 và có độ dài
và có độ dài 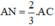
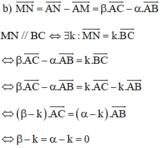
(Do hai vec tơ 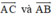 không cùng phương nên chỉ bằng nhau khi chúng đồng thời bằng 0→).
không cùng phương nên chỉ bằng nhau khi chúng đồng thời bằng 0→).
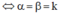
Vậy MN song song với BC khi và chỉ khi α = β.
Xét một vật rắn đồng chất, đẳng hướng và có dạng khối lập phương. Hãy chứng minh độ tăng thể tích ΔV của vật rắn này khi bị nung nóng từ nhiệt độ đầu to đến nhiệt độ t được xác định bởi công thức:
ΔV = V - Vo = βVoΔt
Với Vo và V lần lượt là thể tích của vật rắn ở nhiệt độ đầu to và nhiệt độ cuối t, Δt = t - to, β ≈ 3α (α là hệ số nở dài của vật rắn này).
Chú ý: α2 và α3 rất nhỏ so với α.
+ Gọi V0 là thể tích của khối lập phương ở 0oC:
V0 = l03
+ V là thể tích của khối lập phương ở t0C:
V = l3 = [l0(1+ α∆t)]3 = l03 (1+α∆t)3
Mà (1+ α∆t)3 = 1 + 3α∆t + 3α2∆t2 + α3∆t3
Vì α khá nhỏ nên α2, α3 có thể bỏ qua.
=> V = l3 = l03 (1+ 3α∆t) = Vo (1+ β∆t) với β = 3α.
Gọi V0 là thể tích ở 0oC; V là thể tích ở toC; β là hệ số nở khối. Công thức tính thể tích V ở toC là:
A. V = V 0 / ( 1 + β t )
B. V = V 0 + β t
C. V = V 0 ( 1 + β t )
D. V = V 0 - β t