Cho hàm số f ( x ) = a x 4 + b x 2 + c với a > 0 , c > 2017 và a + b + c < 2017 . Số cực trị của hàm số y = f x - 2017 là
A. 1
B. 5
C. 3
D. 7
cho hàm số y=f(x) có f'(x)=-3(x+4)(x^2-4)(x+1)^2-2x+12 hỏi hàm số f(x) nghịch biến trong khoảng nào sau đây? A. (−∞; -1) B. (0; 2) C. (2; +∞) D. (-1; 0)
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + x + 1,\,\,x \ne 4\\2a + 1,\,\,x = 4\end{array} \right.\)
a) Với a = 0, xét tính liên tục của hàm số tại x = 4.
b) Với giá trị nào của a thì hàm số liên tục tại x = 4?
c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?
a) Với a = 0, tại x = 4, ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2.0 + 1 = 1\\ \Rightarrow \mathop {\lim }\limits_{x \to 4} f\left( x \right) \ne f\left( 4 \right)\end{array}\)
Do đó hàm số không liên tục tại x = 4.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2a + 1\end{array}\)
Để hàm số liên tục tại x = 4 thì \(\mathop {\lim }\limits_{x \to 4} f\left( x \right) = f\left( 4 \right)\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;21{\rm{ }} = {\rm{ }}2a{\rm{ }} + {\rm{ }}1}\\{ \Leftrightarrow \;2a{\rm{ }} = {\rm{ }}20}\\{ \Leftrightarrow \;a{\rm{ }} = {\rm{ }}10}\end{array}\)
Vậy với a = 10 thì hàm số liên tục tại x = 4.
c) TXĐ: \(\mathbb{R}\)
Với \(x\; \in \;\left( {-{\rm{ }}\infty ;{\rm{ }}4} \right)\) có \(f\left( x \right) = {x^2} + x + 1\) liên tục với mọi x thuộc khoảng này.
Với \(x\; \in \;\left( {4;{\rm{ }} + \infty } \right)\) có \(f\left( x \right) = 2a + 1\) liên tục với mọi x thuộc khoảng này.
Do đó hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) khi hàm số \(f\left( x \right)\) liên tục tại điểm x = 4 khi a = 10.
Vậy với a = 10 hàm số liên tục trên tập xác định của nó.
cho hàm số y = f(x) = 5-2x
a) tìm điều kiện của x để hàm số f(x) xác định
b)tính f(-2) ; f(-1) ; f(0) ; f(1/2) ; f(4)
c)tìm x biết f(x) = -4 ; -3 ; 0 ; 5 .
a)Cho hàm số f(x)=ax^2+bx+c là các số hữu thỉ .Chứng tỏ rằng f(-2),f(3)lớn hơn hoặc bằng 0 biết rằng 13a+b+2c=0
b)Cho hàm số f(x) xác định với mọi x thuộc R .Biết rằng với mọi x ta đều có f(x)+3*f(1/x)=x^2
Bài 1: Cho hàm số y =f( x)= -5x -1. Tính f(-1), f(0), f(1), f(1/2)
Bài 2: a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f(-1/2); f(1/2).
b) Cho hàm số y = g(x) = x – 1. Tính g(-1); g(0) ; g(1) ; g(2).
c) Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Lm giúp mình vs mình đang cần gấp .
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
a: f(-2)=7
f(-1)=5
f(0)=3
Câu4 :Cho hàm số y = f(x) = 2x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 6 C. f(-1) = 10 D. f(2) = -4 Câu 5:Một hàm số được cho bẳng công thức y = f(x) = x2 ( x bình phương) Khẳng định nào sau đây đúng? A. f(1) = 6 Câu6:Cho hàm số y = f(x) = 2 + 8x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 10 C. f(-1) = 10 D. f(2) = -4 Câu7:Một hàm số được cho bẳng công thức y = f(x) = 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ A. 0 B. 25 C. 50 D. 10
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Bài 1 : Cho hàm số y = f(x)=\(\frac{a}{2}.x+b\)
a. Tìm a và b biết các điểm sau thuộc đồ thị hàm số : A( -4; -3 ) ; B(0; -3)
b. Tính f(1), f(2) , f(-2), f(-1)
c. Tìm x biết y bằng 4
a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}a\cdot\left(-4\right)+b=-3\\\dfrac{1}{2}a\cdot0+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+b=-3\\b=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-3\\a=0\end{matrix}\right.\)
Vậy: f(x)=-3
b: f(1)=f(2)=f(-2)=f(-1)=-3
c: Đặt y=4
=>f(x)=4
=>-3=4(vô lý)
a) Cho hàm số y=f(x)=-2x+3.Tính f(-2);f(-1);f(0);f(-1/2);f(1/2)
b) Cho hàm số y=g(x)=x^2-1.Tính g(-1);g(0);g(1);g(2)
c)Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Làm bài c thôi ạ mấy câu còn lại nháp thôi ạ.
Cho hàm số f ( x ) = a x 4 + b x 2 + c v ớ i a > 0 , c > 2017 , a + b + c < 2017 . Số cực trị của hàm số y = | f ( x ) - 2017 | là
A. 1
B. 5
C. 3
D. 7
Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:
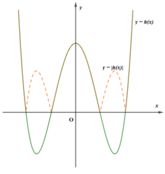
Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
![]()
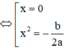
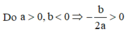
![]()
Ta có: h(0) = c - 2017 > 0, h(-1) = h(1) = a + b + c - 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) - 2017| là 7