Hình hộp ABCD.A'B'C'D' có các cạnh đều bằng a. Tính thể tích V của hình hộp đó biết B A D ^ = D A A ' ^ = B A A ' ^ = 60 °
A. V = a 3 6
B. V = a 3 3 12
C. V = a 3 3
D. V = a 3 2 2
Những câu hỏi liên quan
Cho hình hộp đứng
A
B
C
D
.
A
B
C
D
có tất cả các cạnh đều bằng a,
A
B
C
^
45
0
. Tính thể tích V của khối hộp
A
B
C
D
.
A
B
C
D...
Đọc tiếp
Cho hình hộp đứng A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng a, A B C ^ = 45 0 . Tính thể tích V của khối hộp A B C D . A ' B ' C ' D ' .
Cho hình hộp
A
B
C
D
.
A
B
C
D
có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu của đỉnh
A
trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho. A.
V
4
a
3
2...
Đọc tiếp
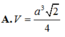
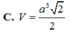
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu của đỉnh A ' trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho.
A. V = 4 a 3 2 3
B. V = 4 a 3 2
C. V = 8 a 3
D. V = 8 a 3 3
Cho hình hộp ABCD.ABCD có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu của đỉnh A trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho. A.
V
4
2
a
3
3
B. ...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu của đỉnh A' trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho.
A. V = 4 2 a 3 3
B. V = 8 2 a 3
C. V = 8 a 3 3
D. V = 8 a 3 3
Chọn B
Ta có: A'O ⊥ (ABCD); OA= A C 2 = a 2
A ' O = A A ' 2 - O A 2 = a 2
V A B C D . A ' B ' C ' D ' = S A B C D . A ' O = 4 a 2 . a 2 = 4 2 a 3
Đúng 0
Bình luận (0)
Tính thể tích của hình hộp ABCD.ABCD biết rằng AABD là tứ diện đều cạnh bằng a. A.
a
3
2
2
B.
a
3
2
4
C.
a
3...
Đọc tiếp
Tính thể tích của hình hộp ABCD.A'B'C'D' biết rằng AA'B'D' là tứ diện đều cạnh bằng a.
A. a 3 2 2
B. a 3 2 4
C. a 3 3 2
D. a 3 2
Cho hình hộp ABCD.A'B'C'D' tất cả các cạnh đều bằng a, góc BAD = 60 độ, hình chiếu vuông góc của A' xuống (ABCD) trùng với trung điểm của AB. Tính thể tích khối hộp ABCD.A'B'C'D'.
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:33
Cho hình hộp \(ABCD.A'B'C'D'\) có độ dài tất cả các cạnh bằng \(a,AA' \bot (ABCD)\) và \(\widehat {BAD} = {60^0}\).
a) Tính thể tích của khối hộp \(ABCD.A'B'C'D'\).
b) Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( {A'BD} \right)\).
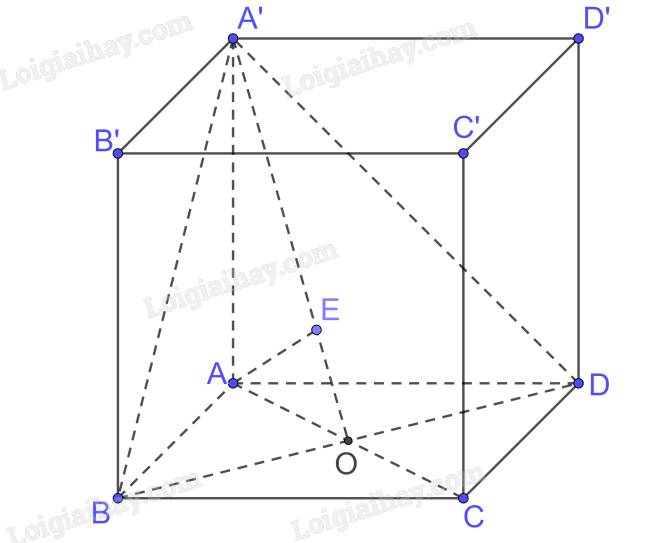
a) Diện tích tam giác ABD bằng diện tích tam giác BCD vì chung đáy BD và chiều cao AO = OC (ABCD là hình thoi)
Diện tích tam giác ABD: \({S_{ABD}} = \frac{1}{2}AB.AD.\sin \widehat {BAD} = \frac{1}{2}a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Rightarrow S = 2{S_{ABD}} = \frac{{{a^2}\sqrt 3 }}{2}\)
Thể tích khối hộp là \(V = AA'.{S_{ABCD}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}\)
b) Gọi \(AC \cap BD = \left\{ O \right\}\)
Ta có \(AA' \bot BD,AO \bot BD \Rightarrow BD \bot \left( {A'AO} \right);BD \subset \left( {A'BD} \right) \Rightarrow \left( {A'AO} \right) \bot \left( {A'BD} \right)\)
\(\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O\)
Trong (A’AO) kẻ \(AE \bot A'O\)
\( \Rightarrow AE \bot \left( {A'BD} \right) \Rightarrow d\left( {A,\left( {A'BD} \right)} \right) = AE\)
Xét tam giác ABD có AB = AD và \(\widehat {BAD} = {60^0}\) nên tam giác ABD đều
\( \Rightarrow OA = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác AOA’ vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{A{{A'}^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{7}{{3{a^2}}} \Rightarrow AE = \frac{{a\sqrt {21} }}{7}\)
Vậy \(d\left( {A,\left( {A'BD} \right)} \right) = \frac{{a\sqrt {21} }}{7}\)
Đúng 0
Bình luận (0)
Cho hình hộp đứng
A
B
C
D
.
A
B
C
D
có đáy là hình vuông cạnh a, AC’ tạo với mặt bên
B
C
C
B
một góc
30
°
. Tính thể tích của khối hộp
A...
Đọc tiếp
Cho hình hộp đứng A B C D . A ' B ' C ' D ' có đáy là hình vuông cạnh a, AC’ tạo với mặt bên B C C ' B ' một góc 30 ° . Tính thể tích của khối hộp A B C D . A ' B ' C ' D ' bằng
A. 2 a 3
B. 2 a 3
C. 2 2 a 3
D. 2 2 a 3
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AA2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
π
a
3
2
Tính thể tích V của hình hộp chữ nhật ABCD.ABCD.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AA 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
πa
3
2
. Tính thể tích V của hình hộp chữ nhật ABCD.ABCD. A.
V
9
a
3
4
B.
V
4
a
3
C. ...
Đọc tiếp
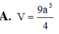
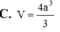
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 πa 3 2 . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
A. V = 9 a 3 4
B. V = 4 a 3
C. V = 4 a 3 3
D. V = 2 a 3
Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .
Đúng 0
Bình luận (0)