Hàm số y = log2 (4x – 2x + m) có tập xác định là ℝ thì
A. m < 1 4
B. m > 0
C. m ≥ 1 4
D. m > 1 4
Hàm số y = log 2 ( 4 x - 2 x + m ) có tập xác định là D = ℝ khi
A . m ≤ 1 4
B . m ≥ 1 4
C . m > 1 4
D . m < 1 4
Chọn C
Hàm số
y
=
log
2
(
4
x
-
2
x
+
m
)
có tập xác định là D =
ℝ
![]()
Đặt ![]() Khi đó, bất phương trình (1) trở thành:
Khi đó, bất phương trình (1) trở thành:
![]()
![]()
Xét hàm số ![]()
Ta có: f'(t) = 2t + 1; f'(t) = 0 ⇔ t = 1 2
Bảng biến thiên:
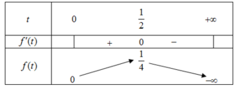
Dựa vào bảng biến thiên, suy ra 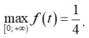
Từ (*) suy ra 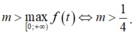
Hàm số y = log 2 ( 4 x - 2 x + m ) có tập xác định là D = R khi
A. m ≤ 1 4
B. m ≥ 1 4
C. m > 1 4
D. m < 1 4
Hàm số y = l o g 2 ( 4 x - 2 x + m ) có tập xác định là D+R khi
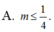
![]()
![]()
![]()
Hàm số y = log 2 ( 4 x - 2 x + m ) có tập xác định là D = R khi
A. m ≤ 1 4
B. m < 1 4
C. m > 1 4
D. m ≥ 1 4
Hàm số y = l o g 2 ( 4 x - 2 x + m ) có tập xác định D = R khi
A. m > 1 4
B. m > 0
C. m ≥ 1 4
D. m < 1 4
Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019;2019) để hàm số sau có tập xác định là D = ℝ
y = x + m + x 2 + 2 ( m + 1 ) x + m 2 + 2 m + 4 + log 2 ( x - m + 2 x 2 + 1 )
A. 2020
B. 2021
C. 2018
D. 2019
Chọn D
Hàm số xác định với mọi ![]() thì
thì  luôn đúng với mọi
luôn đúng với mọi ![]()
+) Ta có: ![]()
![]()
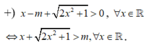
Xét hàm số ![]()
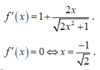
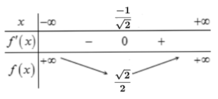
Từ bảng biến thiên ta thấy để 
Kết hợp điều kiện
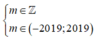
![]()
Kết luận: có 2019 giá trị của m thỏa mãn bài toán.
Cho hàm số y = log2( 4x - 2x + m) có tập xác định D = R khi:
A. m ≥ 1 4
B. m > 1/4
C. m < -1/4
D. m > 0
Chọn B.
Hàm số có tập xác định là D = R khi và chỉ khi 4x - 2x + m > 0 mọi x. (*)
Đặt t = 2x > 0 khi đó (*) trở thành : t2 – t + m > 0 mọi t > 0.
Hay m > t - t2 mọi t > 0
Ta có ![]() suy ra
suy ra ![]()
Hàm số y = log2( 4x- 2x+ m) có tập xác định D= R khi nào?
\(\Leftrightarrow4^x-2^x+m>0;\forall x\)
Đặt \(2^x=t>0\Rightarrow t^2-t+m>0;\forall t>0\)
\(\Rightarrow m>-t^2+t\Rightarrow m>\max\limits_{t>0}\left(-t^2+t\right)=\dfrac{1}{4}\)
Vậy \(m>\dfrac{1}{4}\)
\(y'=\left(2x-2\right)f'\left(x^2-2x\right)=0\Rightarrow\left\{{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
Xét \(f'\left(x^2-2x\right)=0\Rightarrow\left\{{}\begin{matrix}x^2-2x=-2\\x^2-2x=1\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow x=\left\{-1;1-\sqrt{2};1+\sqrt{2};3\right\}\)
Bảng xét dấu:
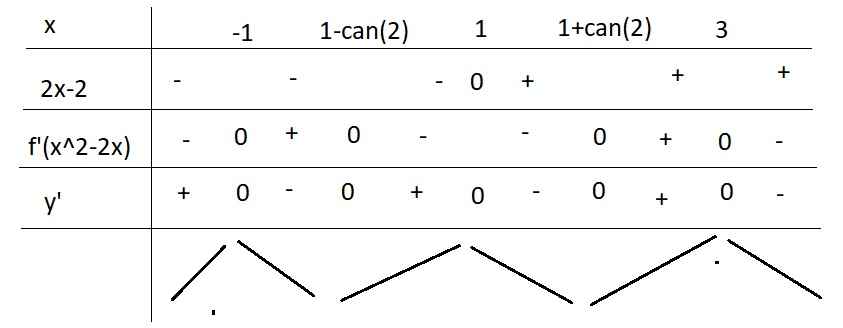
Hàm có 2 cực tiểu (sao khác cả 2 đáp án khoanh thế kia)
Hàm số y = log 2 4 x − 2 x + m có tập xác định là ℝ thì
A. m < 1 4
B. m > 0
C. m ≥ 1 4
D. m > 1 4
Đáp án D
Hàm số có tập xác định là ℝ ⇔ 4 x − 2 x + m > 0 , ∀ x ∈ ℝ ⇔ m > 2 x − 4 x ∀ x ∈ ℝ
Đặt t = 2 x > 0 ⇒ m > t − t 2 ∀ t > 0 ⇔ m > max t > 0 f t ⇔ m > 1 4