Cho số tự nhiên n thỏa mãn C n 2 + A n 2 = 9 n . Mệnh đề nào sau đây là đúng ?
A. n chia hết cho 7
B. n chia hết cho 5
C. n chia hết cho 2
D. n chia hết cho 3
Cho số tự nhiên n thỏa mãn C n 2 + A n 2 = 15 n . Mệnh đề nào sau đây là mệnh đề đúng?
![]()
![]()
![]()
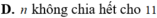
Cho số tự nhiên n thỏa mãn ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A. n chia hết cho 5
B. n chia hết cho 3
C. n chia hết cho 7
D. n chia hết cho 2
Đáp án C
Phương pháp: Sử dụng các công thức
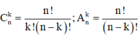
Cách giải: ĐK n ≥ 2
![]()
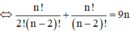
![]()
![]()
Cho số tự nhiên n thỏa mãn C n 2 + A n 2 = 9 n . Mệnh đề nào sau đây đúng?
A. n ⋮ 5
B. n ⋮ 3
C. n ⋮ 7
D. n ⋮ 2
Chọn C
Phương pháp: Sử dụng các công thức 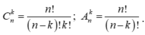
Giải: Điều kiện: n ≥ 2.
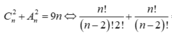
![]()
![]()
Cho số tự nhiên n thỏa mãn C n 2 + A n 2 = 9 n . Mệnh đề nào sau đây đúng?
A. n chia hết cho 5
B. n chia hết cho 3
C. n chia hết cho 7
D. n chia hết cho 2
Đáp án C
Phương pháp: Sử dụng các công thức
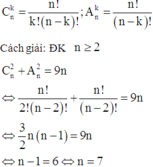
Cho số tự nhiên n thỏa mãn C n 2 + A n 2 = 9 n . Mệnh đề nào sau đây là đúng ?
A. n chia hết cho 7
B. n chia hết cho 5
C. n chia hết cho 2
D. n chia hết cho 3
Đáp án A
C n 2 + A n 2 = 9 n ⇔ n ! 2 ! ( n − 2 ) ! + n ! ( n − 2 ) ! = 9 n ⇔ n ( n − 1 ) 2 + n ( n − 1 ) = 9 n ⇔ 3 n 2 − 21 n = 0 ⇔ n = 0 n = 7
Cho số tự nhiên n thỏa mãn C n 2 + A n 2 = 15 n . Mệnh đề nào sau đây là đúng?
A. n chia hết cho 7
B. n không chia hết cho 2
C. n chia hết cho 5
D. n không chia hết cho 11
Xét hai mệnh đề:
P: “Số tự nhiên n chia hết cho 6”; Q: “Số tự nhiên n chia hết cho 3”.
Xét mệnh đề R: “Nếu số tự nhiên n chia hết cho 6 thì số tự nhiên n chia hết cho 3”.
Mệnh đề R có dạng phát biểu như thế nào?
Thay : “số tự nhiên n chia hết cho 6” bới P, “số tự nhiên n chia hết cho 3” bởi Q, ta được mệnh đề R có dạng: “Nếu P thì Q”
Cho n là số tự nhiên. Xét các mệnh đề:
P: “n là một số tự nhiên chia hết cho 16”.
Q: “n là một số tự nhiên chia hết cho 8”.
a) Với n = 32, phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó.
b) Với n = 40, phát biểu mệnh đề đảo của mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó.
a) Với n = 32, ta có các mệnh đề P, Q khi đó là:
P: “Số tự nhiên 32 chia hết cho 16”;
Q: “Số tự nhiên 32 chia hết cho 8”;
Mệnh đề P ⇒ Q: “Nếu số tự nhiên 32 chia hết cho 16 thì số tự nhiên 32 chia hết cho 8”.
Đây là mệnh đề đúng vì 32 chia hết cho 16 và 8.
b) Với n = 40, ta có các mệnh đề P, Q khi đó là:
P: “Số tự nhiên 40 chia hết cho 16”;
Q: “Số tự nhiên 40 chia hết cho 8”;
Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P: “Nếu số tự nhiên 40 chia hết cho 8 thì số tự nhiên 40 chia hết cho 16”.
Mệnh đề đảo này là mệnh đề sai. Vì 40 chia hết cho 8 nhưng 40 không chia hết cho 16.
cho 3 mệnh đề sau, với n là số tự nhiên
(1) n+ 8 là số chính phương
(2) chữ số tận cùng của n là 4
(3) n-1 là số chính phương
biết hai mệnh đề đúng và 1 mệnh đề sai. hãy xác định mệnh đề nào đúng nào sai
ta thấy 1 số chính phương không bao giờ có đuôi là 2;3;7;8
Mà nếu mệnh đề (2) đúng thì n+8=...2 => mệnh đề (1) sai và n-1=...3 => mệnh đề (3) sai
Nhưng chỉ có 1 mệnh đề sai nên chỉ có mệnh đề (2) là thỏa mãn
Vậy n+8 và n+1 là số chính phương
\(\Rightarrow\left(n+8\right)-\left(n-1\right)=9\)
\(\Leftrightarrow\left(n+8\right)^2-\left(n-1\right)^2=9^2\)
\(\Leftrightarrow\left[\left(n+8\right)-\left(n-1\right)\right]\left[\left(n+8\right)+\left(n-1\right)\right]=9^2\)
\(\Leftrightarrow9\left(2n+7\right)=9^2\)
\(\Leftrightarrow2n-7=9\)
\(\Leftrightarrow n=8\)
Vậy n=8 thì mới thỏa mãn mệnh đề (1) và (3)