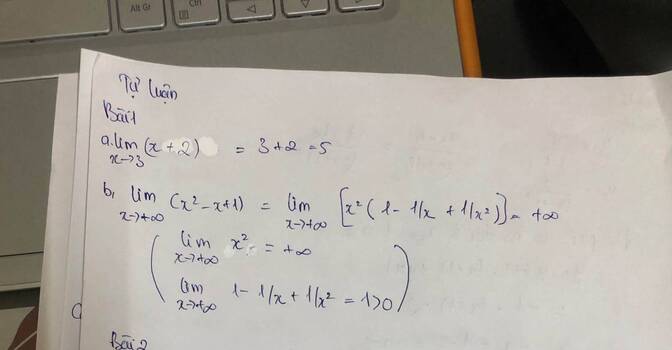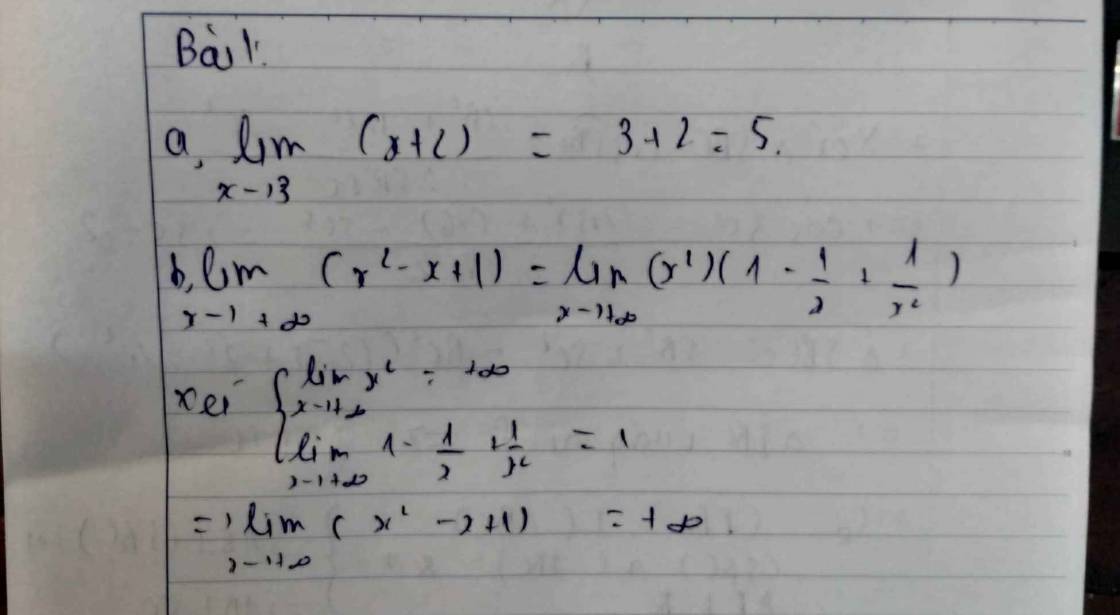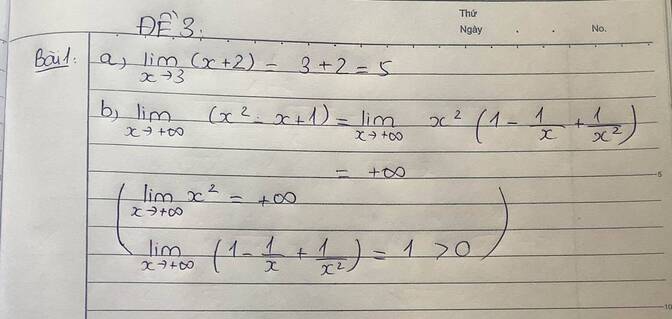Tính các giới hạn sau: lim x → + ∞ 2 x - 6 4 - x

Những câu hỏi liên quan
Tính các giới hạn sau:
a) $\underset{x\to 3}{\mathop{\lim }}\,\left( x+2 \right);$
b) $\underset{x\to +\infty }{\mathop{\lim }}\,\left( {{x}^{2}}-x+1 \right).$
Tính các giới hạn sau :
1/\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{4x^2-3x+1}+2x\right)\)
2/\(lim\left(\sqrt{4n^2+2n+1}-2n+2020\right)\)
2: \(=lim\left(\dfrac{4n^2+2n+1-4n^2}{\sqrt{4n^2+2n+1}+2n}+2020\right)\)
\(=lim\left(\dfrac{2n+1}{\sqrt{4n^2+2n+1}+2n}+2020\right)\)
\(=lim\left(\dfrac{2+\dfrac{1}{n}}{\sqrt{4+\dfrac{2}{n}+\dfrac{1}{n^2}}+2}+2020\right)\)
\(=\dfrac{2}{2+2}+2020=\dfrac{2}{4}+2020=2020.5\)
Đúng 0
Bình luận (1)
tính các giới hạn sau:
a. \(lim\dfrac{\sqrt{x+1}-x+1}{x^2-5x+6}\)
x->3
b. \(lim\left|x^3-3x\right|\)
x->-2
Câu a.
\(^{lim}_{x\rightarrow3}\dfrac{\sqrt{x+1}-x+1}{x^2-5x+6}\)
Nhân liên hợp ta đc:
\(^{lim}_{x\rightarrow3}\dfrac{x+1-\left(x-1\right)^2}{(x^2-5x+6)\cdot\left(\sqrt{x+1}+x-1\right)}\)
\(=^{lim}_{x\rightarrow3}\dfrac{-x^2+3x}{\left(x-3\right)\left(x-2\right)\left(\sqrt{x+1}+x-1\right)}\)
\(=^{lim}_{x\rightarrow3}\dfrac{-x}{\left(x-2\right)\cdot\left(\sqrt{x+1}+x-1\right)}\)
\(=\dfrac{-3}{\left(3-2\right)\cdot\left(\sqrt{3+1}+3-1\right)}=-\dfrac{3}{4}\)
Đúng 1
Bình luận (0)
Câu b.
\(^{lim}_{x\rightarrow-2}\left|x^3-3x\right|\)
\(=\left|\left(-2\right)^3-3\cdot\left(-2\right)\right|=\left|-2\right|=2\)
Câu này đơn giản chỉ thay số thôi nhé, nó ở dạng đa thức nữa!
Đúng 1
Bình luận (0)
Tính các giới hạn
\(\lim\limits_{x\rightarrow1}\dfrac{x^2-\sqrt{x}}{\sqrt{x}-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{2x-\dfrac{1}{2}.x^{-\dfrac{1}{2}}}{\dfrac{1}{2}.x^{-\dfrac{1}{2}}}=\dfrac{2-\dfrac{1}{2}}{\dfrac{1}{2}}=3\)
Đúng 1
Bình luận (0)
Tìm các giới hạn sau:
1/ \(\lim\limits_{x->-1}\) \(\dfrac{x^{2019}+1}{x^2+x}\)
2/ \(\lim\limits_{x->1}\) \(\dfrac{x+x^2+...+x^n-n}{x-1}\)
Lời giải:
1.
\(\lim\limits_{x\to -1}\frac{x^{2019}+1}{x^2+x}=\lim\limits_{x\to -1}\frac{(x+1)(x^{2018}-x^{2017}+x^{2016}-....-x+1)}{x(x+1)}=\lim\limits_{x\to -1}\frac{x^{2018}-x^{2017}+x^{2016}-....-x+1}{x}\)
\(=\frac{(-1)^{2018}-(-1)^{2017}+(-1)^{2016}+....-(-1)+1}{-1}\)
\(=\frac{\underbrace{1+1+....+1+1}_{2019}}{-1}=\frac{2019}{-1}=-2019\)
2.
\(\lim\limits_{x\to 1}\frac{(x-1)+(x^2-1)+(x^3-1)+....+(x^n-1)}{x-1}\\ =\lim\limits_{x\to 1}\frac{(x-1)+(x-1)(x+1)+(x-1)(x^2+x+1)+....+(x-1)(x^{n-1}+x^{n-2}+...+x+1)}{x-1}\)
$\lim\limits_{x\to 1}[1+(x+1)+(x^2+x+1)+....+(x^{n-1}+x^{n-2}+...+x+1)]$
$=1+2+3+....+n=n(n+1):2$
\(\)
Đúng 1
Bình luận (0)
tính các giới hạn sau :a/ \(lim\dfrac{3x^2 3}{x 1}\left(x\rightarrow1\right)\)b/ \(lim\dfrac{2^n 2.4^n}{4.4^n-3.2^n}\)c/ \(lim\dfrac{\left(2n^2 1\right)\left(2n^5 n\right)}{n^7 2}\)d/ \(lim\dfrac{2x 1}{\left(x-2\right)^2}\left(x\rightarrow2\right)\)e...
Đề bị lỗi công thức rồi bạn. Bạn cần viết lại để được hỗ trợ tốt hơn.
Đúng 0
Bình luận (0)
Tính các giới hạn sau:
a) \(\lim\limits_{x\rightarrow1^+}\dfrac{x^3+x+1}{x-1}\)
b) \(\lim\limits_{x\rightarrow-1^+}\dfrac{3x+2}{x+1}\)
c) \(\lim\limits_{x\rightarrow2^-}\dfrac{x-15}{x-2}\)
Lời giải:
a. \(\lim\limits_{x\to 1+}(x^3+x+1)=3>0\)
\(\lim\limits_{x\to 1+}(x-1)=0\) và $x-1>0$ khi $x>1$
\(\Rightarrow \lim\limits_{x\to 1+}\frac{x^3+x+1}{x-1}=+\infty\)
b.
\(\lim\limits_{x\to -1+}(3x+2)=-1<0\)
\(\lim\limits_{x\to -1+}(x+1)=0\) và $x+1>0$ khi $x>-1$
\(\Rightarrow \lim\limits_{x\to -1+}\frac{3x+2}{x+1}=-\infty\)
c.
\(\lim\limits_{x\to 2-}(x-15)=-17<0\)
\(\lim\limits_{x\to 2-}(x-2)=0\) và $x-2<0$ khi $x<2$
\(\Rightarrow \lim\limits_{x\to 2-}\frac{x-15}{x-2}=+\infty\)
Đúng 1
Bình luận (0)
Tính các giới hạn sau: (2 điểm)
a. $\underset{x\to 1}{\mathop{\lim }}\,\frac{{{x}^{3}}+2x-3}{{{x}^{2}}-x}$;
b. $\underset{x\to 1}{\mathop{\lim }}\,\frac{\sqrt{2x+2}-\sqrt{3x+1}}{x-1}$.
\(lim_{x\rightarrow1}\frac{x^3+2x-3}{x^2-x}\)
\(=lim_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2+x+3\right)}{x\left(x-1\right)}\)
\(=lim_{x\rightarrow1}\frac{x^2+x+3}{x}\)
\(=\frac{1^2+1+3}{1}\)
\(=5\)
\(lim_{x\rightarrow1}\frac{\sqrt{2x+2}-\sqrt{3x+1}}{x-1}\)
\(=lim_{x\rightarrow1}\frac{\left(2x+2\right)-\left(3x+1\right)}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{2x+2-3x-1}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-x+1}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-1\left(x-1\right)}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-1}{\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=\frac{-1}{\sqrt{2\cdot1+2}+\sqrt{3\cdot1+1}}\)
\(=\frac{-1}{2+2}=\frac{-1}{4}\)
https://drive.google.com/file/d/14Q-YI3szy-rePnIHWGD35RKCWiCXCT6k/view?usp=sharing
https://drive.google.com/file/d/1425SNt8hu4qt2y1kIcnhIvcxPfODsY1T/view?usp=sharing
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính các giới hạn sau:
1. \(\lim\limits_{x\rightarrow a}\dfrac{x^2-\left(a+1\right)x+a}{x^3-a^3}\)
2. \(\lim\limits_{x\rightarrow1}\left(\dfrac{1}{1-x}-\dfrac{3}{1-x^3}\right)\)
3. \(\lim\limits_{h\rightarrow0}\dfrac{\left(x+h\right)^3-x^3}{h}\)
1: \(A=\dfrac{x^2-\left(a+1\right)x+a}{x^3-a^3}\)
\(=\dfrac{x^2-xa-x+a}{\left(x-a\right)\left(x^2+ax+a^2\right)}\)
\(=\dfrac{\left(x-a\right)\left(x-1\right)}{\left(x-a\right)\left(x^2+ax+a^2\right)}=\dfrac{x-1}{x^2+ax+a^2}\)
\(lim_{x->a}A=lim_{x->a}\left(\dfrac{x-1}{x^2+ax+a^2}\right)\)
\(=\dfrac{a-1}{a^2+a^2+a^2}=\dfrac{a-1}{3a^2}\)
2: \(B=\dfrac{1}{1-x}-\dfrac{3}{1-x^3}\)
\(=\dfrac{-1}{x-1}+\dfrac{3}{x^3-1}\)
\(=\dfrac{-x^2-x-1+3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{-x^2-x+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{-x-2}{x^2+x+1}\)
\(lim_{x->1}\left(B\right)=\dfrac{-1-2}{1^2+1+1}=\dfrac{-3}{3}=-1\)
3: \(C=\dfrac{\left(x+h\right)^3-x^3}{h}=\dfrac{\left(x+h-x\right)\left(x^2+2xh+h^2+x^2+hx+x^2\right)}{h}\)
\(=3x^2+3hx\)
\(lim_{h->0}\left(C\right)=3x^2+3\cdot0\cdot x=3x^2\)
Đúng 0
Bình luận (0)
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right)\);
b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
a) Đặt \(f\left( x \right) = 2{x^2} - x\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to 3\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \left( {2x_n^2 - {x_n}} \right) = 2.\lim x_n^2 - \lim {x_n} = {2.3^2} - 3 = 15\).
Vậy \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right) = 15\).
b) Đặt \(f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to - 1\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \frac{{x_n^2 + 2{x_n} + 1}}{{{x_n} + 1}} = \lim \frac{{{{\left( {{x_n} + 1} \right)}^2}}}{{{x_n} + 1}} = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = - 1 + 1 = 0\).
Vậy \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}} = 0\).
Đúng 0
Bình luận (0)