Cho hình chóp S.ABCD có S A ⊥ ( A B C ) và ∆ A B C vuông ở B. AH là đường cao của ∆ S A B . Khẳng định nào sau đây sai?
A. S A ⊥ B C
B. A H ⊥ B C
C. A H ⊥ A C
D. A H ⊥ S C
Những câu hỏi liên quan
Trong các phát biểu sau, phát biểu nào đúng?a) Hình chóp đều S.ABCD có đáy là hình bình hành.b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Đọc tiếp
Trong các phát biểu sau, phát biểu nào đúng?
a) Hình chóp đều S.ABCD có đáy là hình bình hành.
b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.
c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.
d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Cho hình chóp đều S.ABCD có đường cao bằng 12cm và trung đoạn bằng 13cm. Hãy tính:a) Độ dài cạnh đáy hình chóp;b) Diện tích xung quanh hình chóp;Cho hình chóp đều S.ABCD có đường cao bằng 12cm và trung đoạn bằng 13cm. Hãy tính:a) Độ dài cạnh đáy hình chóp;b) Diện tích xung quanh hình chóp;c) Thể tích hình chópc) Thể tích hình chóp
Đọc tiếp
Cho hình chóp đều S.ABCD có đường cao bằng 12cm và trung đoạn bằng 13cm. Hãy tính:
a) Độ dài cạnh đáy hình chóp;
b) Diện tích xung quanh hình chóp;Cho hình chóp đều S.ABCD có đường cao bằng 12cm và trung đoạn bằng 13cm. Hãy tính:
a) Độ dài cạnh đáy hình chóp;
b) Diện tích xung quanh hình chóp;
c) Thể tích hình chóp
c) Thể tích hình chóp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB a, cạnh đáy CD 2a, AD a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng
3
a
2
2
. Thể tích của hình chóp S.ABCD bằng:A.
a
3
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình bình hành. Hỏi có tất cả bao nhiêu mặt phẳng cách đều 5 điểm S, A, B, C, D ?
A. 2 mặt phẳng.
B. 5 mặt phẳng
C. 1 mặt phẳng
D. 4 mặt phẳng.
Đáp án B
Mặt phẳng cách đều 5 điểm là mặt phẳng mà khoảng cách từ 5 điểm đó đến mặt phẳng là bằng nhau.
Có 5 mặt phẳng thỏa mãn là:
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SBC .
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SAD .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SAB .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SCD .
+ Mặt phẳng đi qua trung điểm của SA,SB,SC,SD.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh a, S A ⊥ (A B C D) ,SC tạo với mặt đáy một góc 60 độ và (SAB ) một góc a với sin a = căn 3/ 4 . Tính chiều cao khối chóp.
Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD
3
a
2
, hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD= 3 a 2 , hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên
S
A
3
a
2
. Tính thể tích khối chóp S.ABCD theo a.
Đọc tiếp
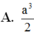
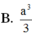
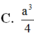
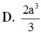
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên S A = 3 a 2 . Tính thể tích khối chóp S.ABCD theo a.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên
S
D
3
a
2
.
Tính thể tích khối chóp
S
.
A
B
C
D
theo a. A.
1
3
a
3
B.
3...
Đọc tiếp
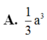
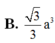
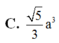
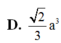
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên S D = 3 a 2 . Tính thể tích khối chóp S . A B C D theo a.
A. 1 3 a 3
B. 3 3 a 3
C. 5 3 a 3
D. 2 3 a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên SD
3
a
2
. Tính thể tích khối chóp S.ABCD theo a. A.
1
3
a
3
B.
3
3
a
3
C.
6...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên SD = 3 a 2 . Tính thể tích khối chóp S.ABCD theo a.
A. 1 3 a 3
B. 3 3 a 3
C. 6 3 a 3
D. 2 3 a 3
Đáp án A
Ta có A D = H A 2 + A D 2 = a 2 2 + a 2 = a 5 2 ⇒ S H = S D 2 - A D 2 = a
Thể tích khối chóp đã cho là: V = 1 3 S H . S A B C D = 1 3 a . a 2 = 1 3 a 3 .
Đúng 0
Bình luận (0)
21 tháng 7 2023 lúc 12:56
Câu 1: Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(4; -1; 2); B(1; 2; 2), C(1; -1; 5)
a) Chứng minh rằng ABC là tam giác đều.
b) Viết Phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC)...
Đọc tiếp
Câu 1: Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C' lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(4; -1; 2); B(1; 2; 2), C(1; -1; 5)
a) Chứng minh rằng ABC là tam giác đều.
b) Viết Phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.
c) Viết phương trình trục của đường tròn ngoại tiếp ΔABC
d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.
các bạn giúp mình với