Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40 ° . Hãy tính: AB
Những câu hỏi liên quan
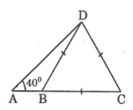
Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40 ° . Hãy tính: AD
cho tam giác BCD là tam giác đều cạnh 5cm và góc DAB bằng 40o. hãy tính AD và AB
Đọc tiếp
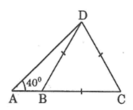
cho tam giác BCD là tam giác đều cạnh 5cm và góc DAB bằng 40o. hãy tính AD và AB
Hình 22.
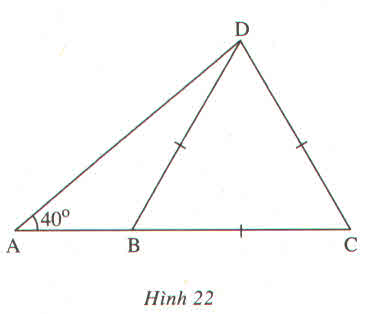
Cho BCD là tam giác đều cạnh 5cm và góc DAB bằng \(40^0\). Hãy tính :
a) AD
b) AB
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
b: XétΔADE vuông tại E có \(AE=AD\cdot\cos A\)
nên AE=5,16(cm)
AB=AE-BE=2,66(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABD là tam giác đều cạnh 5cm và góc DAB = 40 độ . Tính
a, AD
b, AB
tam giác đều thì mỗi góc phải bằng 60o chứ
Đúng 0
Bình luận (0)
bài 6 cho hình thang ABCD (AB//CD). Biết AB=2,5cm; AD=3,5 cm; BD=5cm; và góc DAB bằng góc DAB.
A) Chứng minh: tam giácADB~tam giácBCD
B) Tính độ dài các cạnh BC và CD và tỉ số diện tích của hai tam giác ADB với tam giác BCD
bài 6 cho hình thang ABCD (AB//CD). Biết AB=2,5cm; AD=3,5 cm; BD=5cm; và góc DAB bằng góc DAB.
A) Chứng minh: tam giácADB~tam giácBCD
B) Tính độ dài các cạnh BC và CD và tỉ số diện tích của hai tam giác ADB với tam giác BCD
Cho hình thang ABCD (AB//CD), biết AB =2,5 cm ,AD=3,5 cm , BD =5cm và góc DAB=DBC.
a)Chứng minh 2 tam giác ADB và BCD đồng dạng .
b)Tính độ dài các cạnh BC và CD
c) Tính tỉ số diện tích 2 tam giác ADB và BCD
Cho hình thang ABCD (AB //CD). Biết AB = 2,5cm; AD = 3,5cm; BD = 5cm; và góc DAB = DBC.
a) Chứng minh hai tam giác ADB và BCD đồng dạng.
b) Tính độ dài các cạnh BC và CD
a: Xét ΔADB và ΔBCD có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔADB đồng dạng với ΔBCD
b: ΔADB đồng dạng với ΔBCD
=>AD/BC=DB/CD=AB/BD
=>3,5/BC=5/CD=2,5/5=1/2
=>BC=7cm; CD=10cm
Đúng 0
Bình luận (0)
Cho hình thang ABCD ( AB//CD ). Biết ab = 25cm, AD = 3,5cm, BD = 5cm và góc DAB = góc DBC
a) CM tam giác ADB đồng dạng với tam giác BCD
b) Tính BC và CD
c) Tính tỉ số diện tích tam giác ADB và BCD
a, Xét tam giác ADB và tam giác BCD có
^DAB = ^CBD ; ^ABD = ^CDB ( soletrong)
Vậy tam giác ADB ~ tam giác BCD (g.g)
b, \(\dfrac{AD}{BC}=\dfrac{AB}{BD}\Rightarrow BC=\dfrac{AD.BD}{AB}=\dfrac{7}{10}cm\)
\(\dfrac{DB}{CD}=\dfrac{AB}{BD}\Rightarrow CD=\dfrac{BD^2}{AB}=1cm\)
c, Ta có \(\dfrac{S_{ADB}}{S_{BCD}}=\left(\dfrac{AD}{BC}\right)^2=25\)
Đúng 3
Bình luận (0)