Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng S M N P = 1 2 . M P . N P . sin P

Những câu hỏi liên quan
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng ∆ DNE ∼ ∆ MNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P.
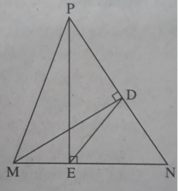
Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên D N M N = E N P N Hai tam giác DNE và MNP đồng dạng vì có góc N chung và D N M N = E N P N
Đúng 0
Bình luận (0)
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng D P = M N . sin N t g P
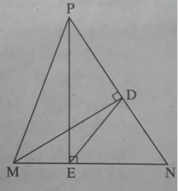
Ta có MD = MN.sinN và MD = DP.tgP nên từ đó suy ra D P = M N . sin N t g P
Đúng 0
Bình luận (0)
Cho tam giác MNP có 3 góc nhọn và MN < MP. Gọi K là trung điểm của NP , E,F lần lượt là chân đường cao kẻ từ N và P , H là trực tâm. S là giao điểm của FE và NP. Chứng minh rằng HS vuoog góc với MK.
Cho tam giác ABC nhọn có 3 đường cao AD BE CF và trực tâm H. Lấy H' đối xứng với H qua BC. Gọi M N là chân đường vuông góc kẻ từ H' đến AB và AC. a, Chứng minh góc AEF=góc ABC. b, CHỨNG MINH EH là tia phân giác của góc DEF và M D N thẳng hàng. c, Gọi S S1 S2 S3 lần lượt là diện tích của các tam giác ABC AEF BDF CDE, chứng minh S1S2S3/S^3 <= 1/64
Cho tam giác MNP có 3 góc nhọn , MN < MP . Gọi I là trung điểm của NP , H,K lần lượt là chân đường cao của tam giác MNP kẻ từ N và P; O là trực tâm. L là giao điểm của HK và NP. Chứng minh : LO vuông góc với MI.
Cho tam giác ABC nhọn, các đường cao AD, BE, CF. Gọi I, K, M,N theo thứ tự là chân đường vuông góc kẻ từ D xuông AB, BE, CF, AC. Chứng minh rằng bốn điểm I, K, M, N thẳng hàng
Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP. Chứng minh
a) Tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA
a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
Do đó: MDHE là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M , đường cao MH . Gọi D,E là chân đường vuông góc hạ từ H xuống MN và MP
a) Chứng minh tứ giác MDHE là hình chữ nhật
b) Gọi A là trung điểm của HP . Chứng minh tam giác DEA vuông
c) T am giác MNP cần thêm điều kiện gì để DE = 2EA
Bài 1 :Cho tam giác ABC nhọn, các đường cao BH,CK. Gọi D và E lần lượt là chân đường vuông góc kẻ từ B,C xuống đường thẳng HK. Chứng minh DK=EH
Bài 2 : Cho tam giác ABC vuông tại A, đường cao AH.Qua trung điểm M của cạnh AC, kẻ MN vuông góc với BC tại N. Gọi K là trung điểm AH. Chứng minh BK vuông góc với AN
Bài 1:
a: Ta có: ΔBKC vuông tại K
mà KM là đường trung tuyến
nên KM=BC/2(1)
Ta có: ΔBHC vuông tại H
mà HM là đường trung tuyến
nên HM=BC/2(2)
Từ (1)và (2) suy ra MH=MK
hay ΔMHK cân tại M
b: Kẻ MN vuông góc với HK
=>N là trung điểm của HK
Xét hình thang CBDE có
M là trung điểm của BC
MN//DB//EC
DO đó: N là trung điểm của DE
=>DK=HE
Đúng 0
Bình luận (0)











