Tọa độ tậm của mặt cầu (S): x 2 + y 2 + z 2 - 10x + 2y +26z + 170 = 0 là
A. (5; -1; -13)
B. (-5; 1; 13)
C. (10; -2; -26)
D. (-10; 2; 26)
Những câu hỏi liên quan
Tọa độ tậm của mặt cầu S : x 2 + y 2 + z 2 - 10 x + 2 y + 26 z + 170 = 0 là
A. (5;-1;-13)
B. (-5;1;13)
C. (10;-2;-26)
D. (-10;2;26)
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
10
x
+
2
y
+
26
z
+
170
0
, tọa độ tâm của (S) là A. (5;-1;-13) B. (-5;1;13) C. (10;-2;-26) D. (-10;2;26)
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 10 x + 2 y + 26 z + 170 = 0 , tọa độ tâm của (S) là
A. (5;-1;-13)
B. (-5;1;13)
C. (10;-2;-26)
D. (-10;2;26)
Cho mặt cầu (S):x^2+y^2+z^2+x-2y+4z-3=0.Xác định tọa độ tâm I của mặt cầu.
Mặt cầu tâm \(I\left(-\dfrac{1}{2};1;-2\right)\)
Đúng 2
Bình luận (0)
Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S):(S):
x
2
+
y
2
+
z
2
– 10x + 2y +26z + 170 0và song song với hai đường thẳng:
d
:
x
-
5
+
2
t...
Đọc tiếp
Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S):
(S): x 2 + y 2 + z 2 – 10x + 2y +26z + 170 = 0
và song song với hai đường thẳng: d : x = - 5 + 2 t y = 1 - 3 t z = - 13 + 2 t v à d ' : x = - 7 + 3 t ' y = - 1 - 2 t z = 8
+ Mặt cầu
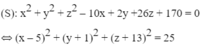
Vậy (S) có tâm I(5; -1; -13), bán kính R = 5.
+ (α) song song với d và d’
⇒ (α) nhận vtcp của d và d’ là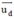 
= (2; -3; 2) và 
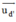= (3 ; -2 ; 0) là các vtcp
⇒ (α) nhận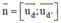 
= (4; 6; 5) là vtpt
⇒ (α): 4x + 6y + 5z + D = 0.
(α) tiếp xúc với (S)
⇒ d(I; α) = R
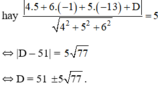
Vậy có hai mặt phẳng thỏa mãn là:
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(
P
)
:
2
x
−
2
y
−
z
−
9
0
và mặt cầu
(
S
)
:
(
x
−
3
)
2
+
(
y
+
2...
Đọc tiếp
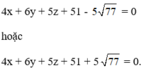
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : 2 x − 2 y − z − 9 = 0 và mặt cầu ( S ) : ( x − 3 ) 2 + ( y + 2 ) 2 + ( z − 1 ) 2 = 100 . Biết (P) cắt (S) theo giao tuyến là một đường tròn. Tìm tọa độ tâm của đường tròn giao tuyến.
A. (3;2;-1)
B. (-3;2;-1)
C. (3;-2;1)
D. (-3;2;1)
Viết phương trình mặt phẳng left(alpharight) tiếp xúc với mặt cầu :
left(Sright):x^2+y^2+z^2-10x+2y+26z+1700
và song song với hai đường thẳng :
d:left{{}begin{matrix}x-5+2ty1-3tz-13+2tend{matrix}right. và d:left{{}begin{matrix}x-7+3ty-1-2tz8end{matrix}right.
Đọc tiếp
Viết phương trình mặt phẳng \(\left(\alpha\right)\) tiếp xúc với mặt cầu :
\(\left(S\right):x^2+y^2+z^2-10x+2y+26z+170=0\)
và song song với hai đường thẳng :
\(d:\left\{{}\begin{matrix}x=-5+2t\\y=1-3t\\z=-13+2t\end{matrix}\right.\) và \(d':\left\{{}\begin{matrix}x=-7+3t'\\y=-1-2t'\\z=8\end{matrix}\right.\)
Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu
x
2
+
y
2
+
z
2
-
10
x
+
2
y
+
26
z
+
170
0
.Và song song với hai đường thẳng
a
:
x...
Đọc tiếp
Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu x 2 + y 2 + z 2 - 10 x + 2 y + 26 z + 170 = 0 .Và song song với hai đường thẳng a : x = - 5 + 2 t y = 1 - 3 t z = - 13 + 2 t , a ' : x = - 7 + 3 t ' y = - 1 - 2 t ' z = 8
Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu
x
2
+
y
2
+
z
2
-
10
x
+
2
y
+
26
z
+
170
0
Và song song với hai đường thẳng
a
:
x...
Đọc tiếp
Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu
x 2 + y 2 + z 2 - 10 x + 2 y + 26 z + 170 = 0
Và song song với hai đường thẳng a : x = - 5 + 2 t y = 1 - 3 t z = - 13 + 2 t và a ' : x = - 7 + 3 t ' y = - 1 - 2 t ' z = 8
A. P : 4 x + 6 y + 5 z + 51 ± 5 77 = 0
B. P : 4 x - 6 y + 5 z + 51 ± 5 77 = 0
C. P : 4 x - 6 y - 5 z + 51 ± 5 77 = 0
D. P : 4 x + 6 y - 5 z - 51 ± 5 77 = 0
Chọn A
Mặt phẳng (P) có vecto pháp tuyến là tích có hướng của hai vecto chỉ phương của hai đường thẳng a và a’. Ta tìm d dựa trên điều kiện mặt cầu tiếp xúc với mặt phẳng.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x - 2y + z + 3 = 0. Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:
A. a + b + c = 8.
B. a + b + c = 5.
C. a + b + c = 6.
D. a + b + c = 7.
