Cho α ∈ ( o ; π 2 ] và thỏa mãn cos α 2 sin 2 α + sin α - 3 = 0 .Tính giá trị của: c o t α 2
A. 1 2
B. 3 2
C.4
D.1
Những câu hỏi liên quan
Cho điểm O và mặt phẳng (α). Chứng minh rằng khoảng cách từ điểm O đến mặt phẳng (α) là bé nhất so với các khoảng cách từ O tới một điểm bất kì của mặt phẳng (α).
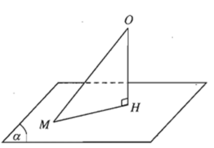
Gọi H là hình chiếu của O lên mặt phẳng (α) ⇒ OH = khoảng cách từ điểm O đến mặt phẳng (α)
M là điểm bất kì thuộc mặt phẳng (α), xét quan hệ giữa đường xiên và hình chiếu OH < OM
Vậy khoảng cách từ điểm O đến mặt phẳng (α) là bé nhất so với các khoảng cách từ O tới một điểm bất kì của mặt phẳng (α).
Đúng 0
Bình luận (0)
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu? A.
R
d
B.
R
2
+
d
2
C.
R
2
-
d
2...
Đọc tiếp
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Chọn C.
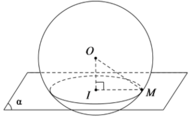
*) Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O; R).
*) Xét tam giác OIM vuông tại I, ta có: OM = R và OI = d nên 
Đúng 0
Bình luận (0)
Cho mặt cầu S(O; R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu? A.
R
d
B.
R
2
+
d
2
C.
R
2
-
d
2...
Đọc tiếp
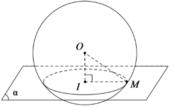
Cho mặt cầu S(O; R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Chọn C.
Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O; R).
Khi d < R thì mặt phẳng cắt mặt cầu (S) theo giao tuyến là đường tròn tâm I bán kính r = IM.
Xét tam giác OIM vuông tại I, ta có: OM = R và OI = d nên
Đúng 0
Bình luận (0)
Cho hình vuông có O là tâm. Có bao nhiêu phép quay tâm O góc α ( 0 ≤ α ≤ π ) biến hình vuông trên thành chính nó?
A.1
B.2
C.3
D.4
Đáp án C
Phép quay tâm O góc quay k. 90 o biến hình vuông thành chính nó.
Đúng 0
Bình luận (0)
Cho tam giác đều có O là tâm. Có bao nhiêu phép quay tâm O góc α ( 0 ≤ α ≤ π ) biến tam giác trên thành chính nó?
A.1
B.2
C.3
D.4
Đáp án B
Phép quay tâm O góc quay k. 120 o biến tam giác đều thành chính nó
Đúng 0
Bình luận (0)
Cho lục giác đều ABCDEF tâm O như hình bên.Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay
α
. Tìm
α
. A.
α
60
0
B.
α
-
60
0
C.
α
120
0
D.
α
-
120...
Đọc tiếp
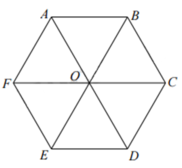
Cho lục giác đều ABCDEF tâm O như hình bên.Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay α . Tìm α .
A. α = 60 0
B. α = - 60 0
C. α = 120 0
D. α = - 120 0
Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay
α
.
Tìm
α
.
A.
α
60
°
B.
α
−
60
°
C.
α
120
°
D.
α
−
120
°
Đọc tiếp
Cho lục giác đều ABCDEF tâm O như hình bên.
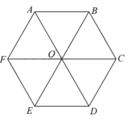
Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay α . Tìm α .
A. α = 60 °
B. α = − 60 °
C. α = 120 °
D. α = − 120 °
Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay α . Tìm α.
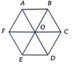
A. 30°
B. 60°
C. 90°
D. 120°
Đáp án D.
Ta có phép quay
Q O ; α A = E ⇔ O A = O E O A ; O E = α ⇒ α = A O E ^ = 120 °
Đúng 0
Bình luận (0)
Cho hình chữ nhật có O là tâm đối xứng. Có bao nhiêu phép quay tâm O góc α
( 0 ≤ α ≤ π ) biến hình chữ nhật trên thành chính nó?
A.0
B.2
C.3
D.4
Đáp án B
Phép quay tâm O góc quay k. 180 o biến hình chữ nhật thành chính nó
Đúng 0
Bình luận (0)
Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc α,0 < α < 2π, biến hình chữ nhật trên thành chính nó?
A. không có
B. một
C. hai
D. vô số
